Precificação de opções exóticas usando Python

As opções exóticas são instrumentos financeiros com características únicas e não padronizadas. Diferentemente das opções de compra e venda tradicionais, padronizadas, conhecidas como opções vanilla, as opções exóticas podem incorporar elementos complexos. Esses elementos incluem mas não estão limitados a cláusulas de barreira, pagamentos condicionais, múltiplos ativos subjacentes e datas de exercício não convencionais. Neste artigo, exploraremos a precificação de opções exóticas usando Python e como essa abordagem pode ser valiosa para investidores e analistas financeiros.

Python e as opções exóticas

Opções exóticas são conhecidas por sua complexidade. Elas podem incluir opções de barreira, opções de cliquet, opções asiáticas, opções de lookback, entre outras. A complexidade reside nas diferentes condições que governam o exercício da opção ou o pagamento do prêmio. Ao contrário das opções europeias e americanas, que podemos usar o modelo de precificação de Black-Scholes, a personalização das opções exóticas requerem abordagens específicas.

Enquanto usamos amplamente o modelo Black-Scholes na precificação de opções tradicionais, sua aplicação ao caso de opções exóticas não é um caminho viável. Precificar opções exóticas é um desafio, mas com a ajuda da linguagem de programação Python, é possível criar modelos para calcular o valor desses instrumentos de forma eficaz.

A linguagem Python pode ser de grande valor devido à sua simplicidade, flexibilidade e uma rica coleção de bibliotecas matemáticas e financeiras. Ela fornece todas as ferramentas necessárias para implementar modelos de precificação personalizados e realizar cálculos complexos. Embora existam bibliotecas financeiras em Python como QuantLib e FinPy, que oferecem funcionalidades específicas para a precificação de derivativos, vamos utilizar uma abordagem baseada na aplicação das funcionalidades mais comuns que fazem parte do “núcleo” da linguagem Python.

Vale muito a pena lembrar que os Certificados de Operações Estruturadas (COEs), fazem bastante uso de opções exóticas em sua composição. Portanto, se você costuma investir nesses produtos, é muito importante aprender a precificar as opções para descobrir se você está pagando muito caro pela montagem da estratégia.

Talvez você também se interesse por:

O que são produtos estruturados?

Métodos de precificação de opções exóticas

A precificação de opções exóticas envolve a criação de modelos que consideram e reproduzem os elementos únicos desses instrumentos. Os métodos mais amplamente utilizados são aqueles que favorecem a implementação de condições dependentes do caminho, como as cláusulas de barreira, por exemplo. Aqui estão dois modelos que podemos implementar em Python para a precificação de opções exóticas:

• Modelo de Árvores Binomiais, que consiste na geração de uma árvore binomial partindo do preço atual do ativo subjacente e evoluindo com base na condição de risco neutro e uma dada volatilidade esperada. Essa dinâmica pode pode ser adaptada para a precificação de opções exóticas, permitindo a inclusão de características específicas, como cláusulas de barreira.
• Método Monte Carlo, que consiste na geração de um grande número de trajetórias aleatórias de preço e no cálculo do valor esperado da opção a partir dessas simulações. O método Monte Carlo é amplamente usado na precificação de opções exóticas, especialmente aquelas com características dependentes do caminho, como é o caso das cláusulas de barreira.

Precificação de opções com cláusula de barreira usando Python

Neste exemplo, vamos considerar o problema de precificar opções de compra e venda com cláusulas de barreira. Para tal, vamos considerar uma volatilidade de \(40\%\), ou \(\sigma=0,40\), taxa de juros livre de risco de 5\% ano ano, composta continuamente, ou r=0,05, o tempo de vida da opção de 45 dias ou, em termos anuais, T=75/252, e o preço de referência do ativo subjacente de R$ 32,00. As características da opção de compra e da opção de venda são dadas abaixo. Para cada uma, vamos definir o preço de exercício, K, a condição de barreira e o gatilho da condição de barreira, G.

1. Put (opção de venda), Strike 110%, \(K_{1}=35,20\), Down and Out 85%, \(G_{1}=27,20\);
2. Call (opção de compra), Strike 110%, \(K_{2}=35,20\), Down and Out 85%, \(G_{2}=27,20\);
3. Call (opção de compra), Strike 100%, \(K_{3}=32,00\), Up and Out 120%, \(G_{3}=38,40\).

Descrição

Nessa descrição, o Strike \(110\%\) representa o preço de exercício igual a \(110\%\) do preço de referência do ativo subjacente. Assim, se o preço de referência do ativo é R$ 32,00, o preço de exercício será \(32,00+10\%=32,00+3,20=35,20\). Por sua vez, a cláusula de barreira de 85%, do tipo Down and Out, significa que se o preço do ativo subjacente atingir 85% do preço de referência, a qualquer momento durante o tempo de vida da opção, a opção deixa de existir. Assim, dado que ambas as opções do exemplo possuem cláusula Down and Out, elas deixam de existir se o preço atingir R$ 27,20 durante o tempo de vida da opção, pois \(32,00\times0,85=27,20\).

Por isso Down (baixa) and (e) out (fora). No momento em que uma opção deixa de existir, seu valor se torna nulo, zero. Por fim, a opção de compra com Strike 100% equivale ao preço atual do ativo, R$ 32,00, e Up and Out 120%, equivalente a R$ 38,40. Assim, se o preço do ativo atingir esse patamar durante o tempo de vida da opção, ela deixa de existir.

Implementação em Python

A seguir, vamos analisar e aplicar um trecho de código em Python que implementa o método Monte Carlo e faz o cálculo do payoff dessas opções. As linhas de comentário informam sobre o propósito de cada bloco de código.

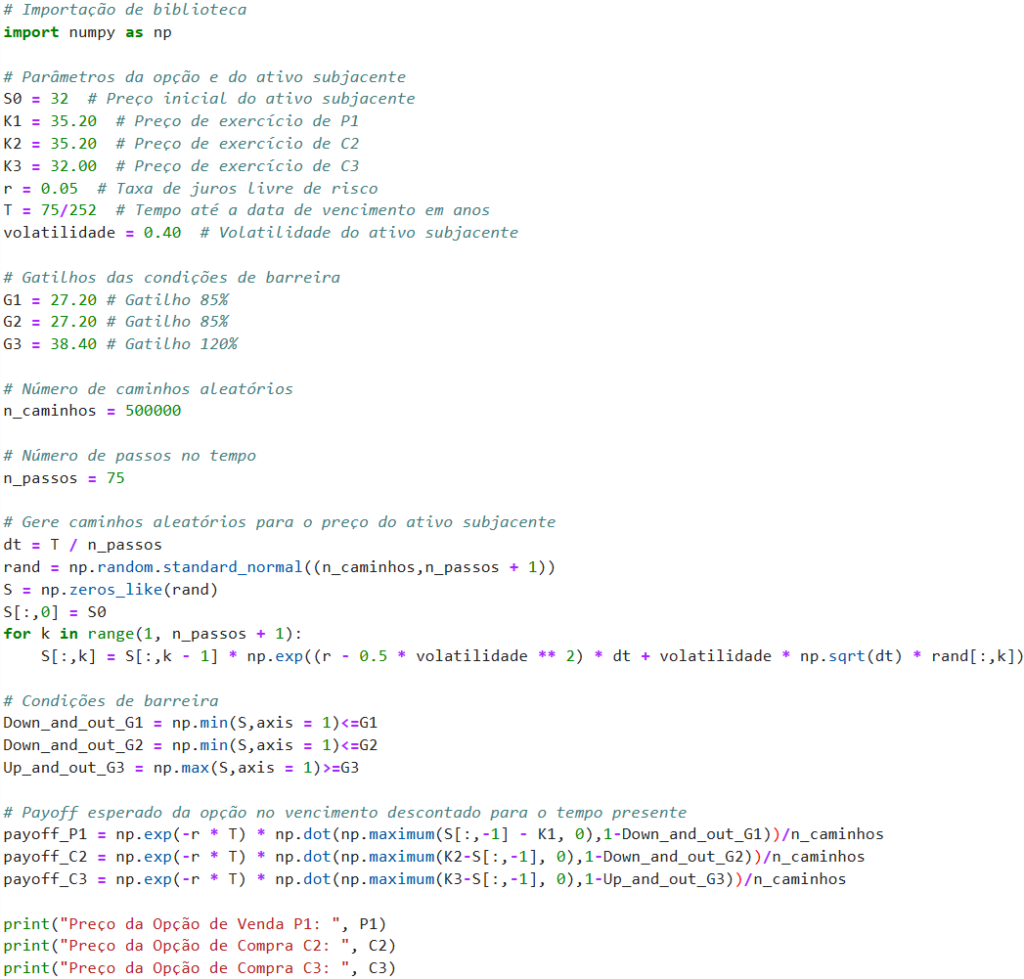
Como resultado do procedimento, encontraremos um valor aproximado do preço atual das opções: \(P_{1}=0,052\), \(C_{2}=3,491\) e \(C_{3}=0,084\). Esses valores correspondem ao valor atual do payoff esperado de cada uma das opções descritas no exemplo, tomando como parâmetro a volatilidade esperada de 40%.

Resumo

Em resumo, neste exemplo realizamos simulações de Monte Carlo para estimar o preço de opções exóticas contendo cláusulas de barreira. O código:

• gera caminhos de preços do ativo subjacente;
• calcula o payoff de cada opção em cada caminho;
• verifica a condição de barreira;
• calcula a média aritmética do payoff de cada opção; e
• faz o desconto para valor presente, utilizando a taxa de juros livre de risco.

Talvez você também se interesse por:

Como calcular as gregas das opções

Negociação Automatizada

Precificação de opções exóticas usando o Excel

Por fim, a precificação de opções exóticas procura calcular o “preço justo” de uma opção exótica, que corresponde ao valor presente do payoff esperado da opção. Devido às condições específicas que podem caracterizar uma opção exótica, o processo de precificação não pode ser realizado por métodos analíticos tradicionais, como o modelo Black-Scholes. É nesse ponto que os modelos implementados em Python podem ser de grande valia. A linguagem Python permite a implementação rápida e simples de modelos e métodos com ênfase numérica, mais versáteis e maleáveis. A partir daí, podemos abordar a precificação de opções exóticas de uma forma prática e de grande utilidade prática.

A combinação de bibliotecas financeiras, a flexibilidade e a capacidade de criar modelos personalizados torna o Python uma escolha poderosa para investidores e analistas que desejam explorar opções para além das opções tradicionais. Com o Python, é possível desenvolver modelos de precificação específicos para atender às características únicas das opções exóticas.