Precificação de opções exóticas usando o Excel

As opções exóticas são instrumentos financeiros complexos e flexíveis, com características únicas, que conferem aos investidores uma ampla gama de possibilidades. Como tal, sua precificação é um processo desafiador em comparação com as opções padrão (também conhecidas como opções vanilla). A precificação das opções exóticas deve levar em conta a variedade de fatores e condições que influenciam e determinam seu valor ao longo do tempo. Neste artigo, exploraremos a precificação de opções exóticas usando o Excel, fornecendo uma visão geral dos conceitos envolvidos e um exemplo detalhado de sua aplicação.

O que são opções exóticas?

Opções exóticas são opções que apresentam características e condições peculiares que não encontramos nas opções vanilla. Opções exóticas diferem das opções vanilla em termos de suas características de pagamento e/ou condições de exercício e até mesmo de existência.

Talvez você também se interesse por:

Usando o Excel para calcular o prêmio de opções

Algumas das cláusulas e características encontradas nas opções exóticas:

• Com Barreira ativam ou desativam a opção quando o preço do ativo subjacente atingir um nível predeterminado, chamado de “barreira” ou “gatilho”. Elas podem ser, por exemplo, do tipo “Up-and-In” (válidas a partir do momento em que o preço sobe e atinge a barreira), “Down-and-Out” (inválidas a partir do momento em que o preço desce e atinge a barreira), “Up-and-Out” (inválidas a partir do momento que o preço sobe e atinge a barreira), ou ainda “Down-and-In” (válidas a partir do momento em que o preço desce e atinge a barreira).
• Opções Asiáticas, em que estabelece-se o valor através da média do preço do ativo subjacente durante um período específico, em vez de seu preço no vencimento.
• Cesta, que se baseiam no desempenho de um conjunto de ativos em vez de um único ativo subjacente.
• Lookback, em que define-se o preço de exercício como o mínimo ou máximo do preço do ativo subjacente durante o período de vida da opção. Daí o termo lookback, ou “olhar para trás”.
• Bermudas, em que os detentores dessas opções podem exercê-las em datas específicas antes do vencimento.

Precificando opções exóticas

Cada tipo de opção exótica tem suas próprias características, que devemos modelar para que a opção possamos precificar a opção. O que elas tem em comum, as opções exóticas, é que seu não podemos calcular seu preço através do clássico modelo Black-Scholes. Vamos partir, então, para uma abordagem numérica, utilizando o Excel e o método Monte Carlo.

Talvez você também se interesse por:

Aplicação do modelo Black-Scholes para a precificação de opções

Como aplicar o método Monte Carlo para a precificação de opções

Precificação de opções exóticas usando Python

Exemplo usando o Excel

Vamos a um exemplo de precificação de uma opção exótica utilizando o Excel.

Neste exemplo, vamos considerar uma opção de compra com cláusula de barreira Up-and-In de \(110\%\). O preço inicial do ativo subjacente é \(S\left(0\right)=100,00\), o preço de exercício da opção \(K=95,00\), a taxa de juros livre de risco de \(8\%\) ao ano, composta continuamente, e tempo de vida igual a \(10\) dias úteis, ou, \(T={10\over{252}}\) em uma base anual em dias úteis, para uma volatilidade esperada para o período equivalente a \(\sigma=40\%\) ao ano. A partir disso, vamos estimar o preço atual da opção de compra utilizando uma simulação Monte Carlo.

Caracterização da cláusula de barreira

Inicialmente, vamos considerar a cláusula de barreira Up-and-In de 110%. Isso significa que a opção será ativada (ou habilitada) se o preço do ativo subjacente atingir 110% do preço de referência, que será o preço atual da ação. Nessas condições, considerando o preço atual de R$ 100,00, temos o gatilho da cláusula de barreira localizado em R$ 110,00. Assim, nesses 10 dias úteis de vida do contrato de opção, se o preço do ativo atingir R$ 110,00, a qualquer momento, a opção de compra passará a existir. Caso contrário, não, e seu payoff será igual a zero.

Entrada de dados na planilha

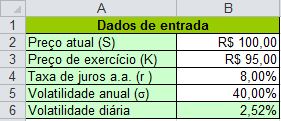
A seguir, vamos entrar os dados em nossa planilha. Para fins da simulação Monte Carlo, utilizaremos dados diários, então precisamos converter a volatilidade anual em diária. Podemos fazer isso com a equação

\[\sigma_{diária}={\sigma_{anual}\over\sqrt{252}}\].\]

Em nossa planilha, na célula B6, devemos digitar \(=B5/RAIZ(252)\) para efetuar esse cálculo.

Simulando as trajetórias de preço

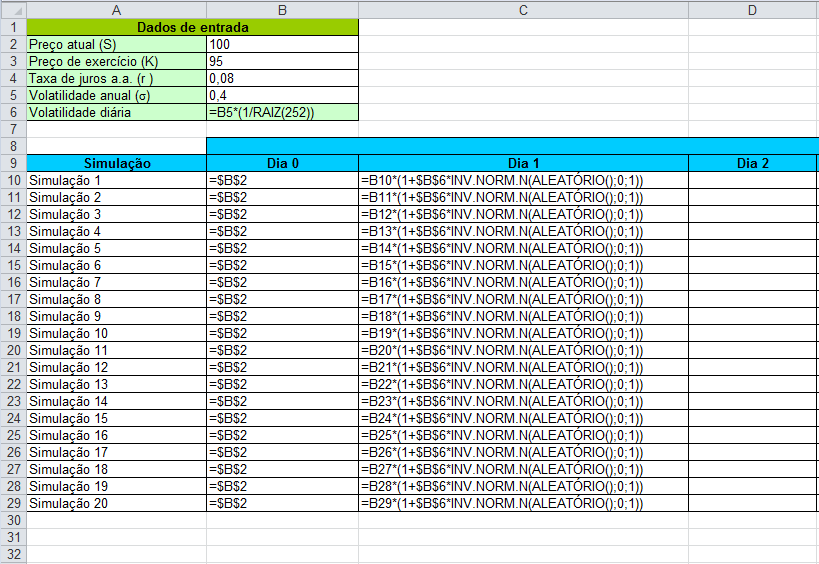
Neste exemplo didático, por simplicidade, vamos considerar a realização de 20 simulações de trajetórias de preços do ativo subjacente. Na prática, esse número deve ser muito maior, possivelmente na casa de alguns milhares ou dezenas de milhares. Em primeiro lugar, vamos atribuir às células de B10 a B29 o valor =$B$2, que é preço atual do ativo subjacente da célula B2. Utilizamos o símbolo $ para travar linha e coluna de nossa célula de referência, e assim podemos utilizar a alça de preenchimento para propagar o valor para as células adjacentes.

A seguir, vamos gerar as trajetórias de preços para cada uma das 20 realizações. Para isso, partiremos do valor presente do ativo e utilizaremos sua volatilidade diária e um elemento de aleatoriedade para gerar os valores subsequentes para cada um dos 10 dias de vida da opção. O elemento de aleatoriedade será gerado pela função INV.NORM.N, que retorna o inverso da distribuição cumulativa normal para a média e o desvio-padrão especificados.

Em nosso caso, utilizaremos a média zero e variância unitária, e multiplicaremos o resultado pela volatilidade diária para obter retornos aleatórios. Utilizando os retornos, calcularemos a trajetória de preços do ativo. Começaremos digitando a equação na célula C10 (Simulação 1, dia 1). Depois, utilizando a alça de preenchimento, podemos propagar a equação para as demais realizações e para os próximos dias.

Avaliando a cláusula de barreira e calculando o payoff de cada trajetória

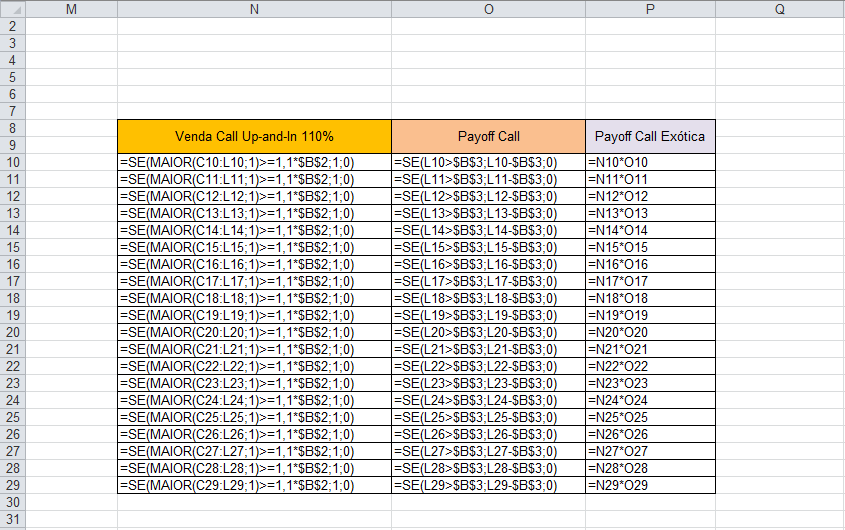
Como próximo passo, precisamos avaliar se a condição de barreira foi ou não atingida, para cada uma das trajetórias. Utilizando a coluna N de nossa planilha, podemos avaliar cada trajetória de preço, buscando o maior preço, e comparar esse resultado ao gatilho da cláusula de barreira. Para procurar o maior preço que trajetória alcançou, utilizaremos a função MAIOR e indicaremos o intervalo de valores que usaremos na avaliação.

No caso da primeira trajetória, o intervalo é de C10 a L10. Para testar se o preço alcançou o gatilho, podemos utilizar a função condicional SE, e atribuir à célula valor 1 em caso verdadeiro e 0 em caso falso. Na coluna O, vamos calcular o payoff de uma opção de compra padrão, e na coluna P utilizaremos as colunas N e O para obter o valor correspondente da opção exótica. Temos agora o payoff da opção de compra exótica para cada uma das trajetórias.

Estimando o preço da opção de compra exótica

Por fim, precisamos calcular o preço da opção de compra exótica. O preço de uma opção, exótica ou não, corresponde ao valor esperado de seu payoff no vencimento, descontado para valor presente. Ou seja, precisamos agora calcular o valor esperado do payoff da opção, que nesse caso corresponde à média aritmética simples do payoff das trajetórias e, a seguir, descontá-lo para o valor presente.

Podemos fazer isso utilizando a função MÉDIA, do Excel e multiplicando o resultado por \(e^{-T\cdot r}=e^{-{10\over{252}}\cdot0,08}\), para descontá-lo para valor presente. No Excel, na célula E2, digitamos =EXP(-10/252*B4)*MÉDIA(P10:P29) para concluir nosso exemplo.

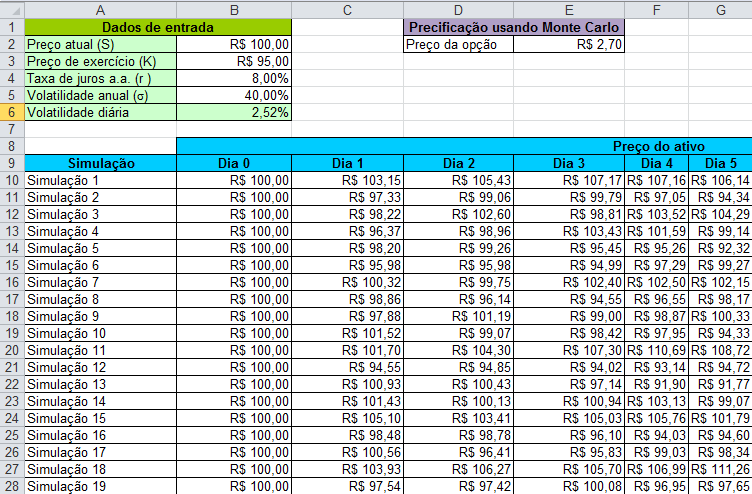
Aumentando o número de simulações para algumas dezenas de milhares temos, portanto, o preço estimado da opção em aproximadamente R$ 2,70. Pronto! Em resumo, temos uma estimativa do preço da opção exótica, calculado usando o Excel!

Resumo

Em resumo, a precificação de opções exóticas envolve um entendimento aprofundado das características e nuances de cada instrumento. Essas características devem ser implementadas em forma de condições na planilha, e as trajetórias devem ser utilizadas para calcular o comportamento do payoff em cada caso. A seguir, o valor esperado dos payoffs (média dos payoffs das trajetórias) deve calculado, utilizando a média aritmética simples. Por fim, o valor esperado do payoff no vencimento deve ser descontado para valor presente, considerando a taxa de juros livre de risco e o tempo de vida da opção.

Por fim, as abordagens numéricas, como o método Monte Carlo, são de grande utilidade por permitirem que as condições e cláusulas das opções exóticas sejam consideradas. Nesse sentido, o uso do Microsoft Excel como ferramenta de modelagem é uma abordagem valiosa para muitos tipos de opções exóticas, permitindo aos investidores e analistas calcular o valor desses derivativos de forma rápida e eficaz.