Usando o Excel para calcular o prêmio de opções
As opções são instrumentos financeiros fascinantes que oferecem aos investidores uma ampla gama de oportunidades de alavancagem e gerenciamento de riscos. Também oferecem um desafio: sua precificação. Uma das tarefas mais críticas ao negociar opções é determinar o preço justo ou o prêmio de uma opção. Portanto, neste artigo, vamos ver como o podemos realizar a precificação de opções forma rápida e efetiva utilizando o modelo Black-Scholes e o Microsoft Excel.
Preliminares: o modelo Black-Scholes
O modelo Black-Scholes é um modelo matemático utilizado para calcular o “preço teórico” de uma opção de compra ou opção de venda. Isso é realizado a partir de alguns parâmetros de entrada:
- Preço do Ativo Subjacente \( S \) é o preço atual da ação, commodity ou índice que é o objeto da opção.
- Preço de Exercício da Opção \( K\) é o preço de referência para o exercício da opção.
- Taxa de Juros Livre de Risco \( r \), geralmente tomada como a taxa básica de juros de uma economia.
- Volatilidade \( \sigma \) é a medida da variação esperada do preço do ativo subjacente ao longo do tempo de vida da opção.
- Tempo de vida da opção \( T \): É o período de tempo até a data de vencimento da opção.
A partir desse parâmetros, utilizando Black-Scholes, podemos calcular o preço de uma opção de compra como
\[C=S\cdot N(d_1)-K\cdot e^{-rT}\cdot N(d_2)\]
em que \(N( . )\) é a função distribuição acumulada e \(d_1\) e \(d_2\) são medidas associadas à probabilidade de a opção ser exercida no vencimento, definidas por
\[d_1 = {ln\left({S\over{K}}\right) + \left(r + {\sigma^2\over{2}}\right)T\over{\sigma\sqrt{T}}}\]
e
\[d2 = d_1 – \sigma\sqrt{T}\]
Analogamente, para uma opção de venda, podemos calcular o preço da opção com a fórmula
\[P=K\cdot e^{-rT}\cdot N(-d_2)-S\cdot N(-d_1)\]
Cálculo do prêmio de opções no Excel
Por exemplo, vamos considerar o preço inicial do ativo subjacente \(S( 0 ) =100,00\), o preço de exercício da opção \(K=95,00\), a taxa de juros livre de risco de 5% ao ano, e tempo de vida igual a 45 dias úteis, ou, \(T= {45\over{252}}\), para uma volatilidade esperada para o período equivalente a σ =40% ao ano.
Vamos à solução, passo-a-passo.
Vamos à solução, passo-a-passo.
Criação da planilha e coleta dos parâmetros de entrada.
Nesta etapa, vamos alocar os dados do problema em nossa planilha, para posteriormente utilizá-los na precificação das opções. Podemos formatar as células com o tipo de dados adequado para cada caso. Temos então,
- primeiro, o tipo de dados Moeda para o preço de ativo subjacente (célula B2) e para o preço de exercício (B3);
- em seguida, o formato Número para o tempo de vida da opção (B4);
- por fim, porcentagem para a volatilidade anual (B5) e taxa de juros livre de risco (B6).
Além disso, vamos renomear as células de B2 a B6 como S, K, T, volatilidade, e r, respectivamente.

Cálculo das probabilidades d 1 e d 2
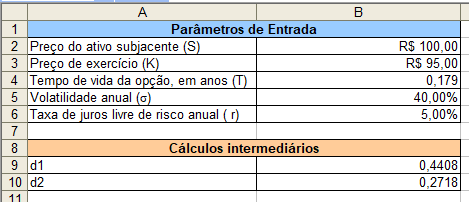
Utilizando as células B9 e B10 para depositar as equações de d 1 e d 2 , temos
- B9 =((LN(S/K) + r+(volatilidade^2)/2)*T)/(volatilidade*RAIZ(T))
- B10 = B9 – volatilidade*raiz(T).
Cálculo das probabilidades acumuladas
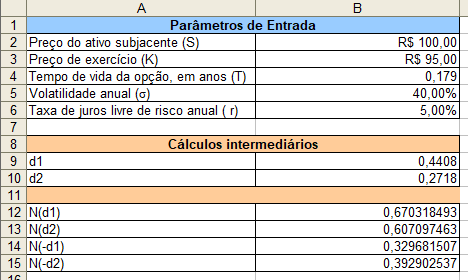
Para o cálculo das probabilidades acumuladas \(N( d_1 )\), \(N( d_2 )\) , \(N( -d_1 )\), \(N( -d_2 )\), vamos utilizar a função DIST.NORM(). Assim, utilizando as células de B12 a B15, temos:
- B12 = DIST.NORM(B9)
- B13 = DIST.NORM(B10)
- B14 = DIST.NORM(-B9)
- B15 = DIST.NORM(-B10).
Cálculo dos prêmios das opções
Por fim, utilizando os elementos que já temos disponíveis, calcularemos o prêmio das opções. Armazenaremos os resultados nas células B18 e B19.
- B18 = S*B12-K*EXP(-r*T)*B13
- B19 =K*EXP(-r*T)*B15-S*B14
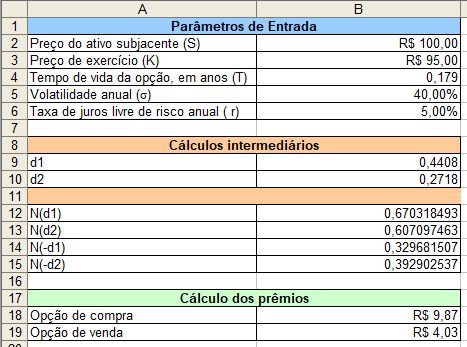
Como resultados, temos os prêmios da opção de compra, R$ 9,87. Por outro lado, o prêmio da opção de venda é R$ 4,03. Alternando para o modo de auditoria de fórmulas no Excel, temos apresentadas todas as equações utilizadas no cálculo do exemplo.
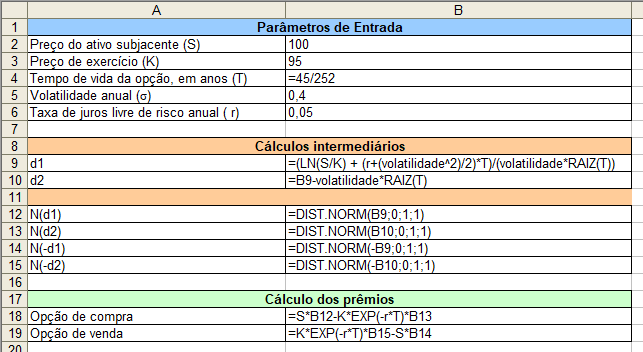
E, pronto! Temos o prêmio das opções calculadas utilizando o modelo Black-Scholes, bem como o Excel.
O Microsoft Excel é uma ferramenta poderosa que facilita o cálculo do prêmio de opções. Neste artigo, exploramos a utilização do modelo Black-Scholes para o cálculo do prêmio de opções. Outros métodos de precificação de opções também podem ser implementados vantajosamente utilizando o Excel, tais como as Árvores Binomiais e o método Monte Carlo.
Essa flexibilidade encontrada nas planilhas eletrônicas permite que os investidores avaliem diferentes cenários e realizem seus próprios estudos acerca de operações, de forma simples e eficaz.