Compreendendo o Modelo Binomial para precificação de opções
A precificação de opções cumpre um papel crucial na tomada de decisões de investimento e gestão de riscos. Dois dos modelos mais amplamente utilizados como base para precificar opções são o modelo binomial ou árvore binomial e o modelo de Black-Scholes. Devido à sua simplicidade, versatilidade e ampla aplicabilidade, o modelo Binomial é uma ferramenta que deve fazer parte do arsenal de todos os investidores que desejam se aprofundar no estudo de opções. Neste artigo, exploraremos o modelo binomial, como ele funciona e por que é uma ferramenta poderosa para precificação de opções.
Entendendo o Modelo Binomial
O modelo Binomial subdivide o tempo de vida da opção em intervalos discretos de tamanhos iguais, a partir do momento presente, e a partir daí traçamos cenários futuros através de sucessivas bifurcações, em um contexto de risco-neutro. O modelo Binomial baseia-se em dois princípios fundamentais:
- A Árvore Binomial, que é uma representação estatística baseada em sucessivas bifurcações utilizadas para traçar trajetórias possíveis da dinâmica de preços do ativo subjacente ao longo do tempo de vida da opção, e as consequentes variações no “preço justo” da opção, que baseia-se no valor esperado do payoff da opção no seu vencimento;
- A probabilidade de Risco-Neutro ou medida martingale considera as probabilidades, eliminando qualquer viés em relação à movimentação de preços futuros e, assim, não proporcionando oportunidades de arbitragem. O payoff esperado equivale apenas à taxa de juros livre de risco.
O objetivo do modelo é proporcionar condições para o cálculo do “preço justo” de uma opção a partir da expectativa do valor do payoff dessa opção no vencimento. Para tal, o modelo binomial baseia-se na criação da Árvore Binomial da evolução de preços do ativo subjacente e no cálculo do payoff da opção para cada ponto do último nível da árvore. Considera-se que o valor presente da medida desses payoffs é uma boa aproximação para o “preço justo” da opção.
Como o Modelo Binomial precifica opções?
Investidores, frequentemente, usam o modelo binomial para precificar opções de compra e opções de venda. Tanto do tipo de exercício Europeu (exercício no vencimento) quanto do tipo Americano (exercício a qualquer momento, até o vencimento). O processo de precificação começa com o valor presente do ativo subjacente e sua volatilidade histórica. Podemos calcular a volatilidade histórica através da série temporal de retornos do ativo.
A partir disso, devemos construir a árvore binomial correspondente, para o número de períodos desejado, estimando os preços do ativo subjacente em cada nível da árvore com base na volatilidade do ativo e na duração do período. Fazemos isso levando em consideração a probabilidade neutra ao risco de subida e descida nos preços do ativo. Veja um exemplo na imagem abaixo:
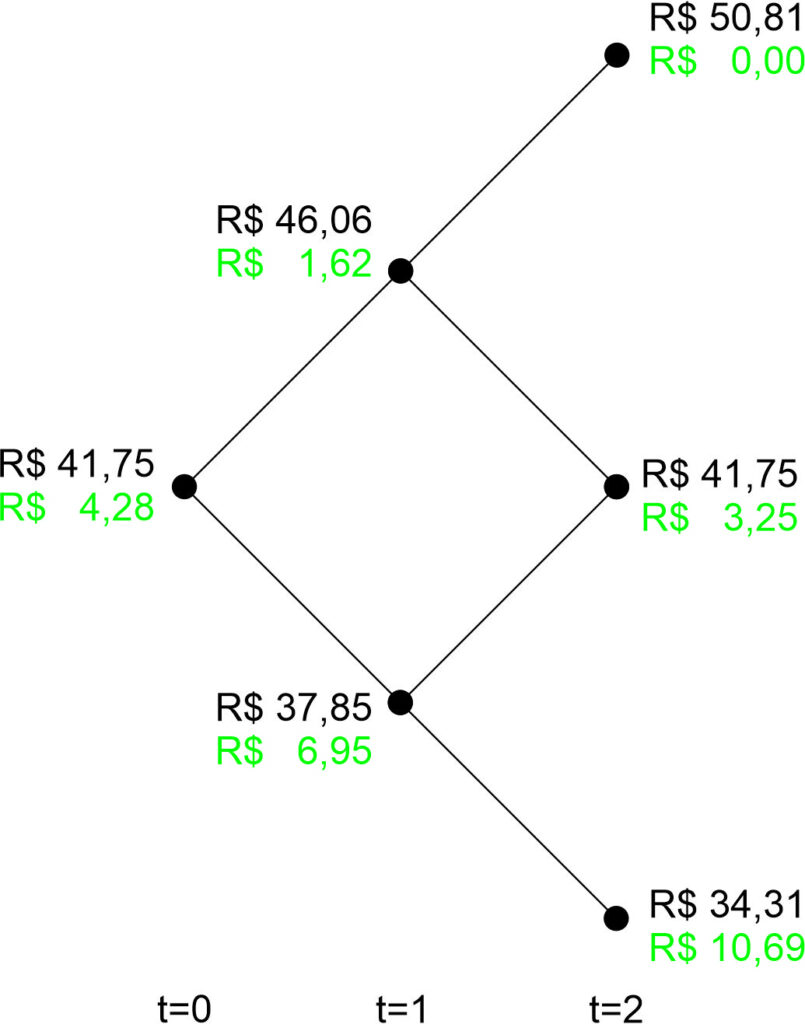
Na última etapa da árvore, correspondente ao vencimento da opção, calcula-se o valor da opção de compra para cada trajetória. Faz-se isso utilizando-se a equação de payoff da opção. Retrocedendo na árvore, calcula-se o valor de cada opção em cada bifurcação anterior, utilizando-se o valor esperado do payoff da opção, descontado para valor presente. Para tal, é necessário descontar a “deriva” dos valores causada pela aplicação à taxa de juros livre de risco. Lembre-se de que o princípio da probabilidade de risco-neutro postula que o payoff esperado equivale tão somente à taxa de juros livre de risco.
Retrocedendo-se na árvore e calculando-se o valor da opção de compra em cada ponto anterior envolve a aplicação da fórmula de precificação retroativamente. Por fim, trazemos tais valores retroativamente a valor presente descontando-os pela taxa de juros livre de risco. O valor resultante é o “preço justo” da opção.
Por Que o Modelo Binomial é Importante?
Podemos adaptar o modelo Binomial para acomodar diferentes complexidades, incluindo o tipo de exercício das opções americanas (que podemos exercer a qualquer momento antes do vencimento) e opções com múltiplos períodos de vencimento. Os modelos analíticos de precificação de opções não permitem acomodar tais complexidades devido às hipóteses propostas na formulação do problema. Relaxando as hipóteses, por outro lado, tornamos o problema insolúvel.
Assim, o modelo Binomial é importante porque permite contornar as dificuldades analíticas e manter a abordagem simples. Além disso, podemos argumentar que o funcionamento do modelo é altamente intuitivo, proporcionando excelentes exemplos didáticos e introdutórios para investidores interessados em compreender o processo de precificação de opções. Definitivamente, sob o ponto de vista didático, esse é o primeiro modelo que se deve para entender precificação.
O modelo Binomial também tem suas limitações. A principal delas é o fato de que ele pode gerar precificações imprecisas caso o passo temporal escolhido não seja pequeno o suficiente. Nesse caso, o payoff esperado da opção será calculado sobre um conjunto menor de dados e estará sujeito a imprecisões. Ou seja, o modelo é sensível ao número de subdivisões escolhido para o tempo de vida da opção.
Além disso, outro aspecto, de menor relevância, é que o modelo não considera dividendos. No caso das opções negociadas na B3, isso não é problemático porque o valor dos dividendos é descontado do preço de exercício de todas as séries de opções disponíveis. Assim, na prática, essa limitação não se aplica ao caso de opções cujo preço de exercício quando descontamos os dividendos.
 Talvez você também se interesse por:
Talvez você também se interesse por:Conclusão
Em resumo, o modelo binomial é uma ferramenta valiosa e amplamente utilizada na precificação de opções. Sua versatilidade é um atrativo especial, tendo em vista que permite acomodar opções com diferentes características sem maiores complicações. Além disso, é um enfoque bastante intuitivo e adequado para iniciantes no mundo das opções, tendo em vista que facilita compreensão do processo de precificação.