Aplicação do Modelo Binomial para precificação de opções
Um dos modelos mais amplamente utilizados para precificar opções é o modelo Binomial. Esse status se deve à sua combinação única de simplicidade, versatilidade e aplicabilidade. O modelo Binomial subdivide o tempo de vida da opção em intervalos discretos de tamanhos iguais, a partir do momento presente. A partir daí, traçamos cenários futuros através de sucessivas bifurcações equiprováveis, em um contexto de risco neutro. Neste artigo, exploraremos a aplicação do modelo Binomial, trabalhando com um exemplo e sua solução passo-a-passo, com o objetivo de compreendermos em detalhes o seu funcionamento.
Princípios do Modelo Binomial
O modelo Binomial baseia-se em dois princípios:
- A Árvore Binomial: é uma representação gráfica de sucessivas bifurcações equiprováveis, utilizadas para traçar trajetórias possíveis dos preços a partir de uma dada volatilidade. Assim, a partir do preço em um momento \(t\) , definido por \(S( t )\), podemos calcular os preços no próximo nível da Árvore Binomial multiplicando o preço atual pelas possibilidades equiprováveis de alta (up), \(u\) , ou baixa (down), \(d\) , definidas por:
\[\begin{equation}
\begin{array}{ccl}
u&=& e^{\sigma\sqrt{\Delta t}}\\
d&=& e^{-\sigma\sqrt{\Delta t}}
\end{array}
\end{equation}\]
em que \(\Delta t\) é o comprimento do período correspondente a um nível da Árvore Binomial, e \(\sigma\) é a volatilidade histórica do ativo, comumente utilizada em termos anuais; - A probabilidade de Risco-Neutro ou medida martingale: é uma abordagem que considera as probabilidades envolvidas de tal forma que qualquer viés em relação à movimentação de preços futuros do ativo subjacente é eliminada, não havendo oportunidade de arbitragem e considerando que o payoff esperado equivale tão somente à taxa de juros livre de risco, que denotaremos por \(r\).
Criação da Árvore Binomial
A criação da Árvore Binomial da evolução de preços do ativo subjacente é o primeiro passo. Mas, como chegar a esses valores? Vamos denotar o preço do ativo subjacente como \(S(t)\), e considerar o preço no instante inicial, \(t=0\), como \(S(0)=41,75\). Vamos também considerar que o período é dado em meses e que a volatilidade anual do ativo será considerada \(\sigma =0,34\), e a taxa de juros livre de risco \( r=5,50\%\) ao ano, equivalente a \(5,35\%\) capitalizada continuamente. Em nosso caso,
\[\begin{equation}
\begin{array}{ccccl}
u&=&e^{0,34\sqrt{1/12}}&=&1,103128\\
d&=&e^{-0,34\sqrt{1/12}}&=&0,906513
\end{array}
\end{equation}\]
\begin{array}{ccccl}
u&=&e^{0,34\sqrt{1/12}}&=&1,103128\\
d&=&e^{-0,34\sqrt{1/12}}&=&0,906513
\end{array}
\end{equation}\]
Daqui a um mês, quando \(t= {1\over{12}}\), teremos \(\Delta t= {1\over{12}}\) (um mês, ou um doze avos de um ano, já que a volatilidade é anualizada). Então temos em nossa Árvore duas possibilidades equiprováveis para \(t= {1\over{12}}\):
- o preço do ativo subjacente será igual a \(S({1\over{12}})=S( 0 ) \cdot u=41,75e^{0,34 \sqrt{{1\over{12}}}} =46,06\) ; ou
- o preço do ativo subjacente será igual a \(S({1\over{12}})=S( 0 ) \cdot u=41,75e^{-0,34 \sqrt{{1\over{12}}}} =37,85\)
Teremos uma bifurcação para cada uma dessas possibilidades quando \(t=2\), e então:
- o preço do ativo subjacente será igual a \(S({2\over{12}})=S( {1\over{12}} ) \cdot u=46,06e^{0,34 \sqrt{{1\over{12}}}} =50,81\) ; ou
- o preço do ativo subjacente será igual a \(S({2\over{12}})=S( {1\over{12}} ) \cdot d=46,06e^{-0,34 \sqrt{{1\over{12}}}} =41,75\) ; ou
- o preço do ativo subjacente será igual a \(S({2\over{12}})=S( {1\over{12}} ) \cdot u=37,85e^{0,34 \sqrt{{1\over{12}}}} =41,75\) ; ou
- o preço do ativo subjacente será igual a \(S({2\over{12}})=S( {1\over{12}} ) \cdot d=37,85e^{-0,34 \sqrt{{1\over{12}}}} =34,31\) .
Preenchendo esses valores nas trajetórias correspondentes, temos a Árvore Binomial mostrada na figura abaixo:
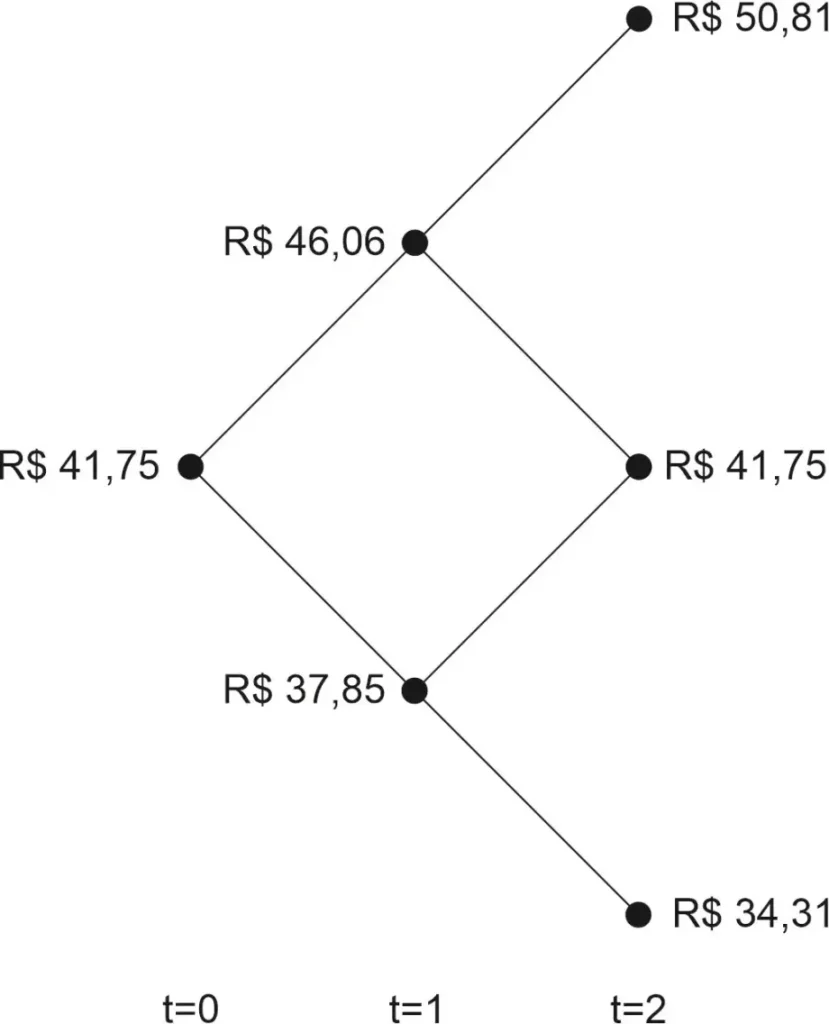
Como o Modelo Binomial precifica opções?
Vamos considerar uma opção de venda com preço de exercício \(K\) igual a \(R\$45,00\), ou seja, \(K=45\), e com vencimento para daqui a dois meses, ou seja, em \(t= {1\over{12}}\). Na última etapa da árvore, correspondente ao vencimento da opção, vamos calcular o valor da opção de venda para cada uma das trajetórias, através da função de payoff \(P\) para opções de venda. Se \(K>S\) no vencimento da opção de venda, então \(P=K-S\). Caso contrário, \(P=0\), ou seja, a opção vence sem valor ou “vira pó”.
Começando pelo fim
O processo de precificação deve ser aplicado do fim para o começo da árvore. Então, aplicando-se essa função payoff aos valores finais da árvore, em \(t= {1\over{12}}\), temos o preço da opção de venda em cada caso:
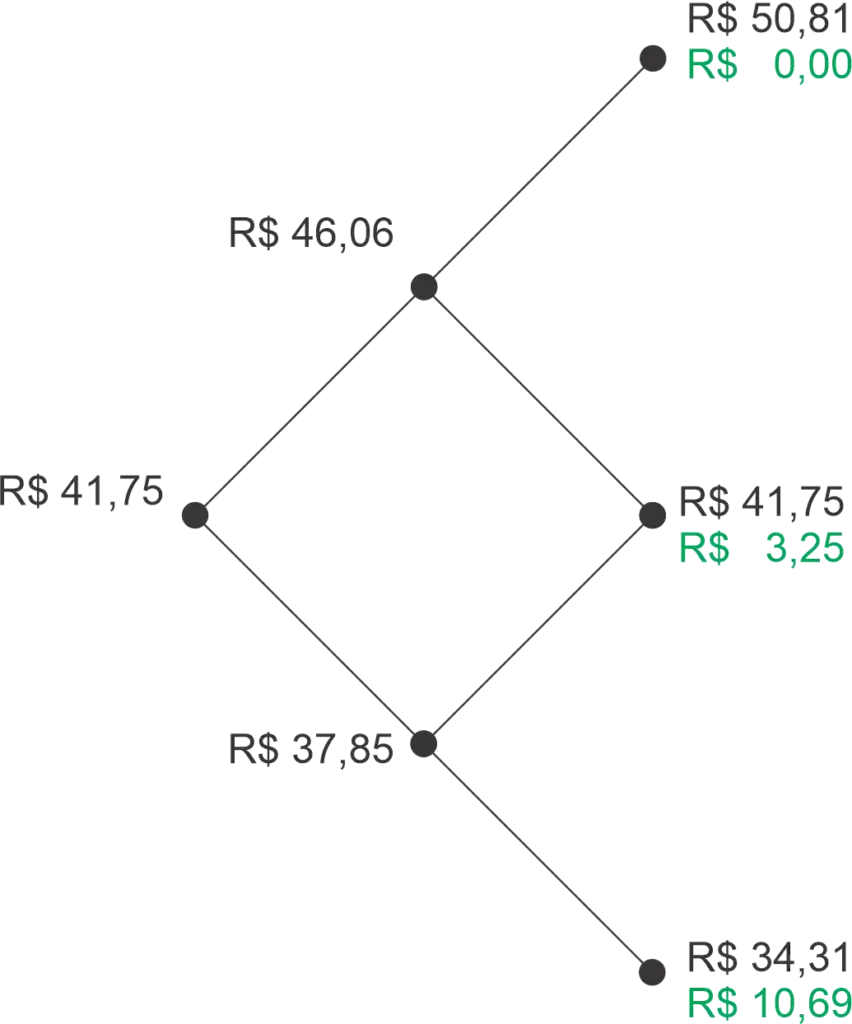
- Para \(S=50,81\), temos \(45,00<50,81\), então \(V=0,00\), ou seja, a opção de venda vence fora do dinheiro ou “vira pó”;
- Para \(S=41,75\), temos \(45,00>41,75 \), então \(V=3,25\);
- Para \(S=34,31\), temos \(45,00>34,31\), então \(V=10,69\).
Esses casos e valores estão representados na figura abaixo:
Dando um passo atrás
Vamos voltar um passo e precificar as opções no período anterior. Para tal, precisamos considerar a deriva do valor esperado da opção, denotada por \(\pi\), e definida como: \(\pi = {e^{r\Delta t}-d}\over{u-d}\) que em nosso exemplo resulta em \(\pi =0,4982\).
Assim, temos o valor da opção no primeiro nível da árvore, em \(t= {1\over{12}}\), para cada caso:
- Para \(S=46,06\), a opção de venda encontra-se fora do dinheiro, porém está a 1 mês do vencimento. O payoff esperado pode ser calculado como
\[\begin{equation}
\begin{array}{rcl}
V & = & e^{-r\cdot\Delta t}\left[\pi V_{u}+\left(1-\pi\right)V_{d}\right]\\
& = & e^{-0,0535\cdot\frac{1}{12}}\cdot\left[0,4982\cdot0,00+\left(1-0,4982\right)\cdot3,25\right]\\
& = & 1,62
\end{array}
\end{equation}\] - Para \(S=37,85\), a opção de venda encontra-se dentro do dinheiro, e a 1 mês do vencimento. O payoff esperado é
\[\begin{equation}
\begin{array}{rcl}
V & = & e^{-r\left(\triangle t\right)}\left[\pi V_{u}+\left(1-\pi\right)V_{d}\right]\\
& = & e^{-0,0535\cdot\frac{1}{12}}\cdot\left[0,4982\cdot3,25+\left(1-0,4982\right)\cdot10,69\right]\\
& = & 6,95
\end{array}
\end{equation}\]
Essa etapa da precificação é apresentada na figura:
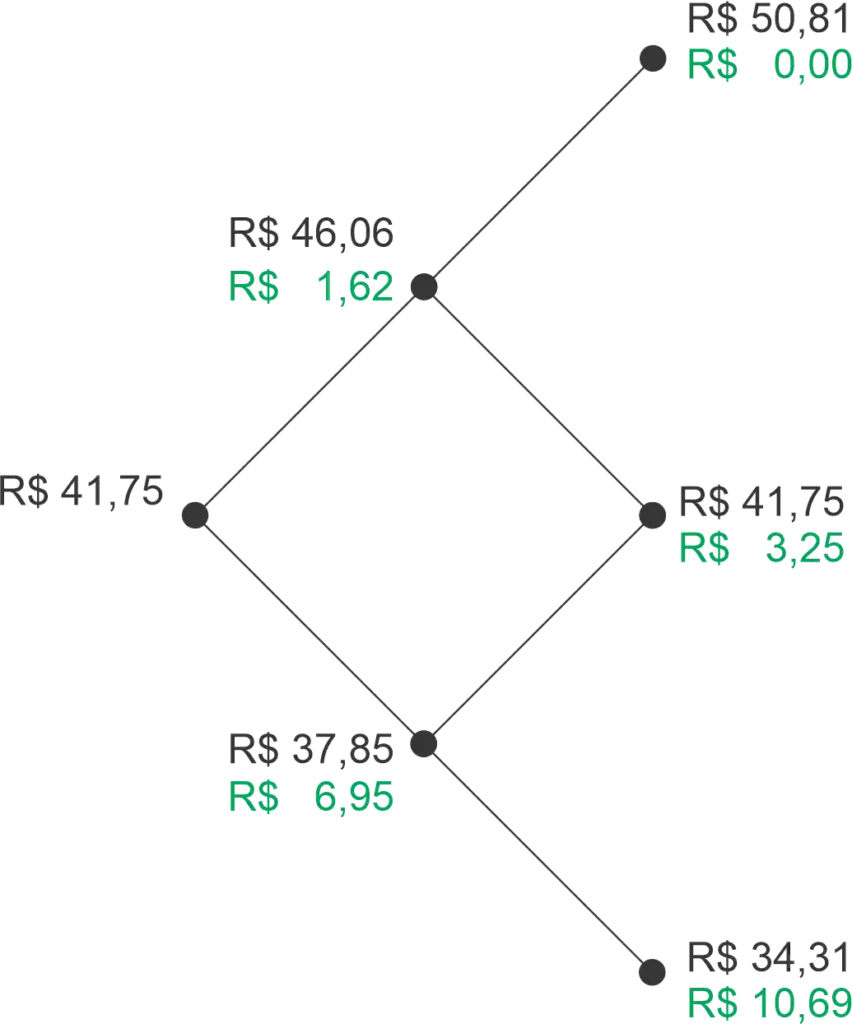
Chegando no começo: o valor presente
Finalmente, repetindo-se o procedimento anterior, o preço atual da opção de venda é dado por
\[\begin{equation}
\begin{array}{rcl}
V & = & e^{-r\left(\triangle t\right)}\left[\pi V_{u}+\left(1-\pi\right)V_{d}\right]\\
& = & e^{-0,0535\cdot\frac{1}{12}}\cdot\left[0,4982\cdot1,62+\left(1-0,4982\right)\cdot6,95\right]\\
& = & 4,28
\end{array}
\end{equation}\]
\begin{array}{rcl}
V & = & e^{-r\left(\triangle t\right)}\left[\pi V_{u}+\left(1-\pi\right)V_{d}\right]\\
& = & e^{-0,0535\cdot\frac{1}{12}}\cdot\left[0,4982\cdot1,62+\left(1-0,4982\right)\cdot6,95\right]\\
& = & 4,28
\end{array}
\end{equation}\]
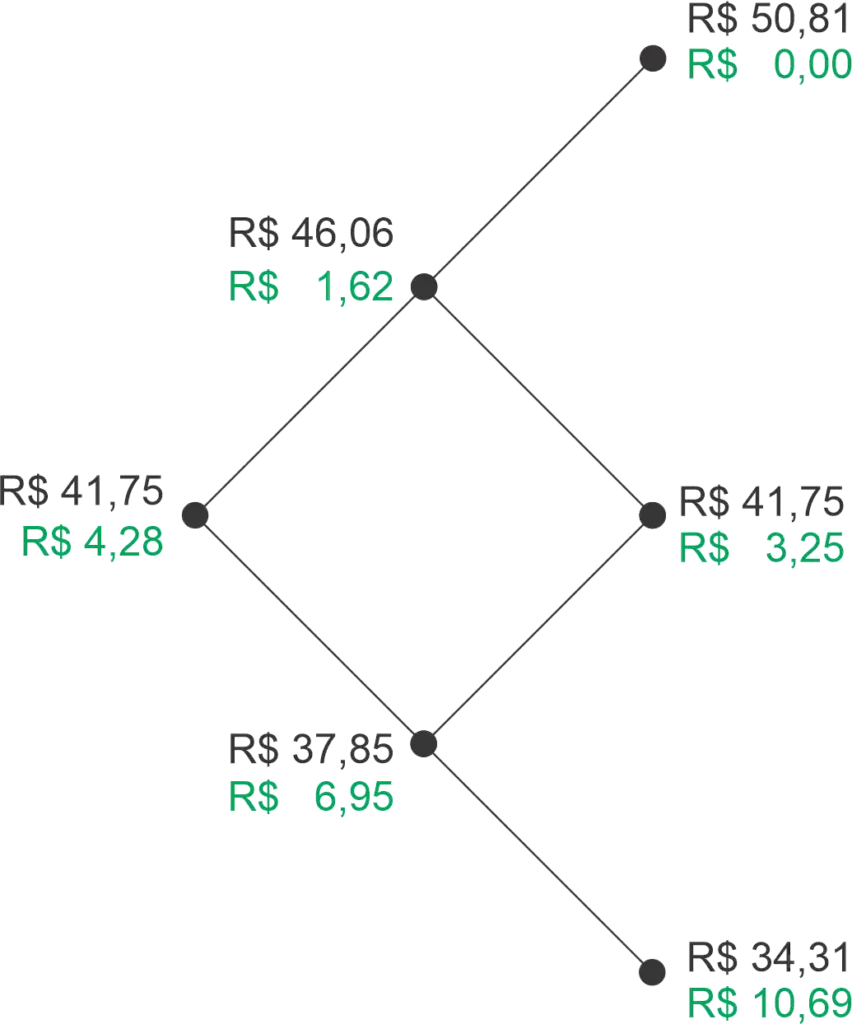
Através do modelo Binomial, concluímos que a opção de venda vale atualmente R$ 4,28. Nas mesmas condições, o modelo Black-Scholes resultaria em R$ 4,08. Qual é o motivo da discrepância? O motivo é o baixo número de períodos em que dividimos o tempo de vida da opção de venda. Na medida em que aumentamos o número de subdivisões do tempo de vida, o valor entregue pelo modelo Binomial tende a aproximar-se do valor resultante do cálculo por Black-Scholes.
Por Que o Modelo Binomial é importante?
Podemos adaptar o modelo Binomial para acomodar diferentes complexidades, incluindo opções americanas (aquelas que o investidor pode exercer a qualquer momento antes do vencimento) e opções com múltiplos períodos de vencimento.
Quem já estudou os modelos analíticos de precificação de opções sabe que acomodar tais complexidades na formulação do problema comumente torna-o insolúvel. Assim, o modelo Binomial é importante porque permite contornar as dificuldades analíticas e manter a abordagem simples.
Além disso, podemos argumentar que o funcionamento do modelo é altamente intuitivo, proporcionando excelentes exemplos didáticos e introdutórios para investidores interessados em compreender o processo de precificação de opções. Definitivamente, sob o ponto de vista didático, é o primeiro modelo que devemos estudar para esse fim.
O modelo Binomial também tem suas limitações. A principal delas é o fato de que ele pode gerar precificações imprecisas caso o passo temporal escolhido não seja pequeno o suficiente, caso em que o payoff esperado da opção será calculado sobre um conjunto menor de dados.
Ou seja, o modelo é sensível ao número de subdivisões que escolhemos para o período de vida da opção. Outro aspecto, de menor relevãncia, é que o modelo não considera dividendos. No caso das opções negociadas na B3, isso não é problemático porque o valor dos dividendos é descontado do preço de exercício de todas as séries de opções disponíveis.
 Talvez você também se interesse por:
Talvez você também se interesse por:Em resumo, o modelo Binomial é uma ferramenta valiosa e amplamente utilizada na precificação de opções. Sua versatilidade é um atrativo especial, tendo em vista que permite acomodar opções com diferentes características sem maiores complicações. Além disso, é um enfoque bastante intuitivo e adequado para iniciantes no mundo das opções, tendo em vista que facilita compreensão do processo de precificação.