Cálculo das gregas no Excel
O cálculo das Gregas em opções é uma parte essencial da gestão de risco e estratégias de negociação. As Gregas referem-se a um conjunto de medidas da sensibilidade das opções às mudanças nas variáveis do mercado, como preço do ativo subjacente, volatilidade, tempo até o vencimento e taxas de juros. Neste artigo, exploraremos como realizar o cálculo das gregas usando o Excel.
O modelo Black-Scholes e as Gregas
As Gregas são as taxas de variação no preço de uma opção em relação a variações nos parâmetros relevantes para sua precificação. Isso inclui o preço do ativo subjacente, tempo de vida da opção, bem como a volatilidade e a taxa de juros. Para o caso de opções vanilla européias, as Gregas podem ser calculadas de forma analítica a partir de derivadas parciais do modelo Black-Scholes em relação a seus parâmetros:
- S é o preço atual do ativo subjacente;
- V é o preço atual da opção sobre o ativo;T é o tempo de vida restante da opção;
- \(\sigma\) é a volatilidade anual;
- r é a taxa de juros livre de risco ao ano.
Esses parâmetros influenciam na precificação das opções de formas diferentes. Portanto, é essa sensibilidade do preço da opção a variações nos parâmetros que as Gregas buscam mensurar.
Talvez você também se interesse por:
Usando o Excel para calcular o prêmio de opções
Calculando as Gregas em Python
O Cálculo das Gregas
Delta
O Delta mede a sensibilidade do preço de uma opção a mudanças no preço do ativo subjacente. O Delta varia de 0 a 1 para opções de compra e de -1 a 0 para opções de venda. Um Delta de 0,50 significa que, para cada aumento de R$ 1,00 no preço do ativo subjacente, o preço da opção aumentará em, aproximadamente, R$0,50. Em termos matemáticos, Delta é definido como:
\[\Delta=\frac{\partial V}{\partial S}\]
Em termos práticos, o Delta para uma opção de compra é calculado como
\[\Delta_{call}=\frac{\partial V}{\partial S}=N\left(d_{1}\right).\]
Por outro lado, para uma opção de venda, temos
\[\Delta_{put}=\frac{\partial V}{\partial S}=-N\left(-d_{1}\right)\]
em que N(.) é a função de distribuição de probabilidade acumulada, e
\[d_{1}=\frac{ln\left(\frac{S}{K}\right)+\left(r+\frac{1}{2}\sigma^{2}\right)\cdot T}{\sigma\sqrt{T}}.\]
Gamma
O Gamma mede a taxa de variação do Delta de uma opção em relação às mudanças no preço do ativo subjacente. Em outras palavras, ele quantifica a sensibilidade do Delta em relação às mudanças no preço do ativo subjacente. O Gamma é particularmente importante para os traders que usam estratégias de hedge, como delta hedging. Quanto maior o Gamma, mais rápido o Delta da opção muda em resposta a mudanças no preço do ativo subjacente. Em termos matemáticos, o Gamma é definido como
\[\Gamma=\frac{\partial}{\partial S}\left(\Delta\right)=\frac{\partial^{2}V}{\partial S^{2}}.\]
Portanto, calculando-se essa derivada parcial, obtemos
\Gamma=\frac{1}{\sqrt{2\pi}\cdot S\cdot\sigma\cdot\sqrt{T}\cdot e^{\frac{d_{1}^{2}}{2}}}
Vega
Vega mede a sensibilidade do preço de uma opção às mudanças na volatilidade implícita do ativo subjacente. A volatilidade implícita representa as expectativas do mercado em relação à volatilidade futura do ativo subjacente. Uma opção com alto Vega é sensível às mudanças na volatilidade, o que a torna uma escolha atraente para os investidores que acreditam que a volatilidade aumentará. Por outro lado, uma opção com baixo Vega é menos sensível às mudanças na volatilidade, tornando-a mais adequada para investidores que esperam que a volatilidade diminua. Em termos matemáticos, Vega é definida como
\[\nu=\frac{\partial V}{\partial\sigma}\]
que resulta em
\[\nu=\frac{S\cdot\sqrt{T}\cdot e^{-\frac{d_{1}^{2}}{2}}}{\sqrt{2\pi}}\]
Theta
O Theta mede a sensibilidade do preço de uma opção à passagem do tempo. À medida que o tempo passa, o valor de uma opção tende a diminuir, e o Theta quantifica essa deterioração do valor da opção. O Theta é uma medida crítica para os compradores de opções, pois indica quanto valor uma opção pode perder diariamente devido à passagem do tempo. Para opções de curto prazo, o Theta tende a ser menor, enquanto para opções de longo prazo, o Theta é mais significativo. No entanto, à medida que uma opção se aproxima da data de vencimento, o Theta aumenta significativamente.
\[\Theta=\frac{\partial V}{\partial t}\]
que resulta em
\[\Theta=r\cdot V-r\cdot S\cdot\Delta-\frac{1}{2}\cdot\sigma^{2}\cdot S^{2}\cdot\varGamma.\]
Rho
Rho mede a sensibilidade do preço de uma opção às mudanças nas taxas de juros. Geralmente, opções de compra têm Rho positivo, o que significa que seus preços aumentam à medida que as taxas de juros sobem. Por outro lado, opções de venda têm Rho negativo, o que significa que seus preços diminuem com o aumento das taxas de juros. No entanto, o impacto do Rho nas opções geralmente é menos significativo em comparação com outras Gregas, a menos que haja mudanças drásticas nas taxas de juros.
\[\rho=\frac{\partial V}{\partial r}\]
Teremos, portanto
\[\rho=K\cdot T\cdot e^{-rT}\cdot N\left(d_{2}\right),\]
em que
\[d_{2}=d_{1}-\sigma\sqrt{T}\]
Cálculo das Gregas em Excel: um exemplo
Neste exemplo, vamos considerar o preço inicial do ativo subjacente \(S\left(0\right)=100,00\), o preço de exercício da opção \(K=95,00\), a taxa de juros livre de risco de \(5\%\) ao ano, e tempo de vida igual a 45 dias úteis, ou, \(T=\frac{45}{252}\), para uma volatilidade esperada para o período equivalente a \(\sigma=40\%\) ao ano. O preço atual das opções de compra e venda, calculados através do modelo Black-Scholes: C=9,87 e P=4,03. Com esses dados, vamos calcular as Gregas de uma opção de compra e de uma opção de venda sobre o ativo.
Em primeiro lugar, vamos dispor os dados de entrada nas células de B2 a B6. No entanto, para facilitar a referência aos valores de entrada, vamos renomear as células de B2 a B6 como S, K, T, volatilidade e r, respectivamente.
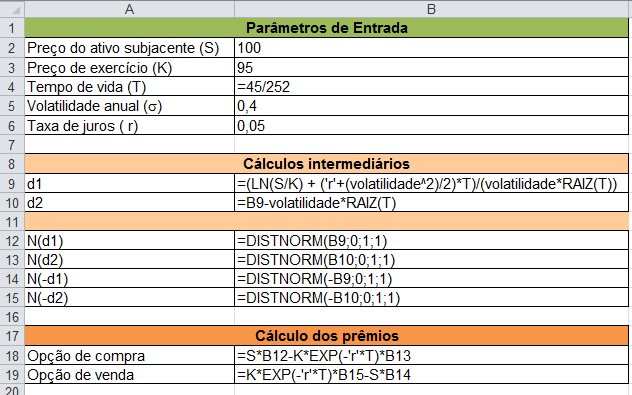
A seguir, devemos fazer os cálculos intermediários para obter os valores de \(d_{1}\) e \(d_{2}\), seguindo as equações apresentadas anteriormente (células B9 e B10). A partir disso, nas células B12 a B15, calculamos as distribuições acumuladas, utilizando a função DISTNORM e indicando média zero, variância unitária e modo cumulativo. Por fim, será necessário calcular os prêmios das opções, utilizando o modelo Black-Scholes. O prêmio das opções foi calculado nas células B18 e B19.
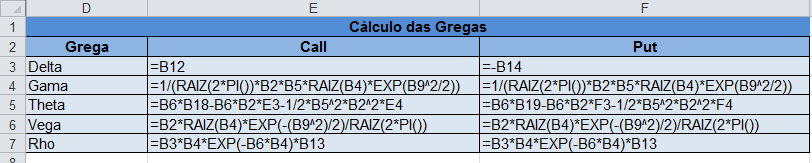
Para calcular as Gregas, utilizaremos as células de E3 a F6 e utilizaremos as fórmulas apresentadas na seção anterior. Esse procedimento é mostrado na figura abaixo, em que aparecem as fórmulas no formato do Excel. Alternativamente, ao invés de indicar as células de B2 a B6, podemos utilizar o nome atribuído a cada célula, S, K, T, volatilidade e r, respectivamente.
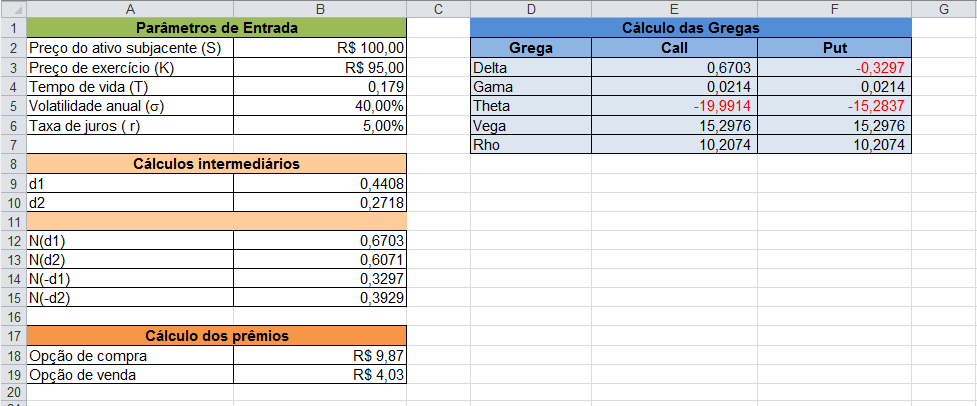
E, pronto! Temos nossa planilha do Excel com os valores de todas as Gregas. Se desejarmos mudar os Parâmetros de Entrada, então teremos o recálculo dos prêmios das opções e também das Gregas correspondentes!
Resumo
Neste artigo, tratamos do cálculo das Gregas em Excel, e incluímos um exemplo para ilustrar o procedimento, em detalhes. As Gregas são de fundamental importância para compreender o efeito de mudanças nas condições de mercado sobre o preço das opções.
Conhecer e saber como calcular as Gregas é fundamental para a montagem e manutenção de estratégias de hedging, e o Excel é uma ferramenta que facilita sobremaneira essa tarefa.
