Delta das opções: sensibilidade ao preço
Se você deseja tornar-se um especialista no mercado de opções, é imprescindível que você conheça o modelo de precificação de Black & Scholes e, em particular, que você conheça as variáveis, ou gregas, do modelo. Uma dessas variáveis é o delta das opções, que mede a sensibilidade do preço da opção em relação à variação do preço da ação. É sobre essa variável que falaremos no presente artigo.
O que é o delta
O delta da opção é a variável que mede a razão entre a mudança de preço da opção e a mudança de preço da ação. Matematicamente,
\[\Delta={{H_{o_n}-L_{o_n}}\over{H_{a_n}-L_{a_n}}}\]
em que
- \(H_{a_n}\) é o preço de máxima (High) da ação em um determinado pregão n.
- \(L_{a_n}\) é o preço de mínima (Low) da ação no pregão n.
- \(H_{o_n}\) é o preço de máxima (High) da opção em um determinado pregão n.
- \(L_{o_n}\) é o preço de mínima (Low) da opção no pregão n.
Em outras palavras, um delta de 30%, significa que se a ação variar R$ 0,10, a opção irá variar R$ 0,03.
Formalmente falando, o delta significa o quanto o preço de uma opção mudará para uma variação infinitesimal no preço da ação. Ou seja, para uma variação em uma casa decimal localizada infinitamente distante à direita da vírgula. Na prática, acabamos por considerar variações de alguns centavos no preço da ação, principalmente se o volume operado for muito grande.
Delta de uma call
O preço de uma call aumenta à medida que o preço da ação aumenta. Por exemplo:
| Dia | Máxima da ação | Mínima da ação | Máxima da call | Mínima da call | Fechamento da ação | Fechamento da call |
| 1 | 34,71 | 33,85 | 1,69 | 1,16 | 34,13 | 1,26 |
| 2 | 34,62 | 34,07 | 1,59 | 1,26 | 34,21 |
Podemos calcular o para o dia 1. Teríamos, então
\[\Delta={{H_{o_n}-L_{o_n}}\over{H_{a_n}-L_{a_n}}}={{1,59-1,26}\over{34,62-34,07}}={{0,33}\over{0,55}}=0,610=61,0\%\]
Com isto, e sabendo que a ação subiu R$ 0,08 (preço de fechamento) do dia 1 para o dia 2, podemos calcular o novo preço da opção.
Como o delta da opção é de 61,0%, o novo preço da opção será:
\[Preço_{novo}=Preço_{antigo}+\Delta\cdot Variação_{ação}\]
Ou seja
\[Preço_{novo}=R\$ 1,26+60%\cdot R\$ 0,08=R\$ 1,26+R\$ 0,05=R\$ 1,31\]
Aqueles familiarizados com a disciplina de cálculo talvez tenham notado que o delta é a taxa de variação do preço da opção em relação ao preço da ação, ou seja, o delta é a derivada do preço da opção em relação ao preço da ação.
Isso significa que o delta mede a inclinação da reta tangente ao gráfico de variação do preço da opção em relação ao preço da ação.
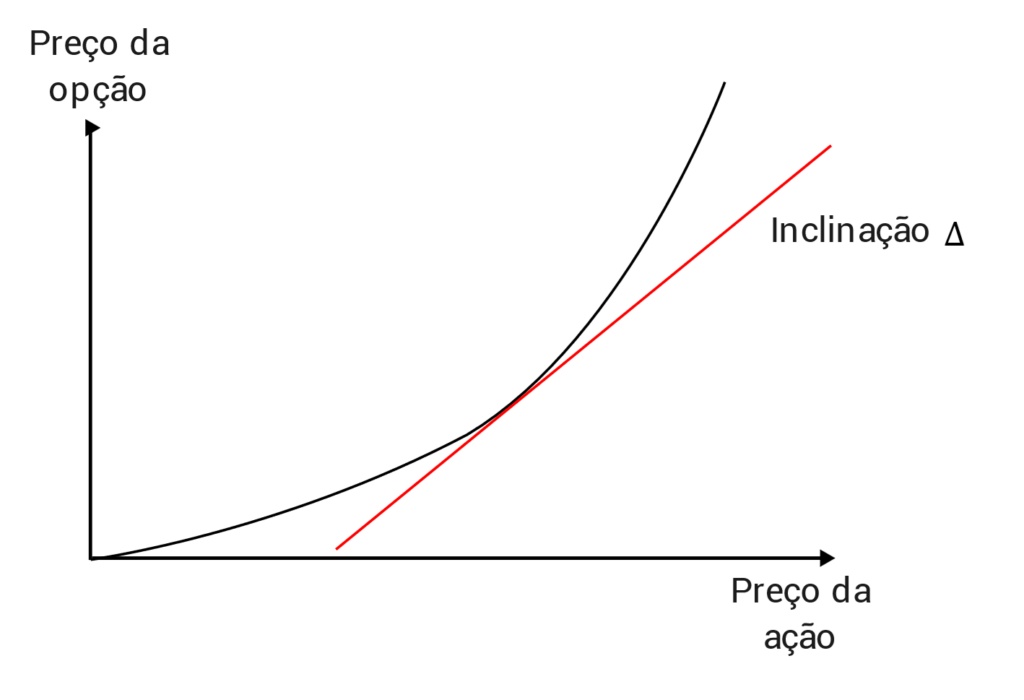
Observe que quanto mais o preço da ação sobe, maior será a inclinação da reta tangente, ou seja, maior será o delta. No limite, o delta se aproxima de 1 (ou 100%), o que significa que se a ação variar R$ 1,00 a opção também irá variar R$ 1,00.
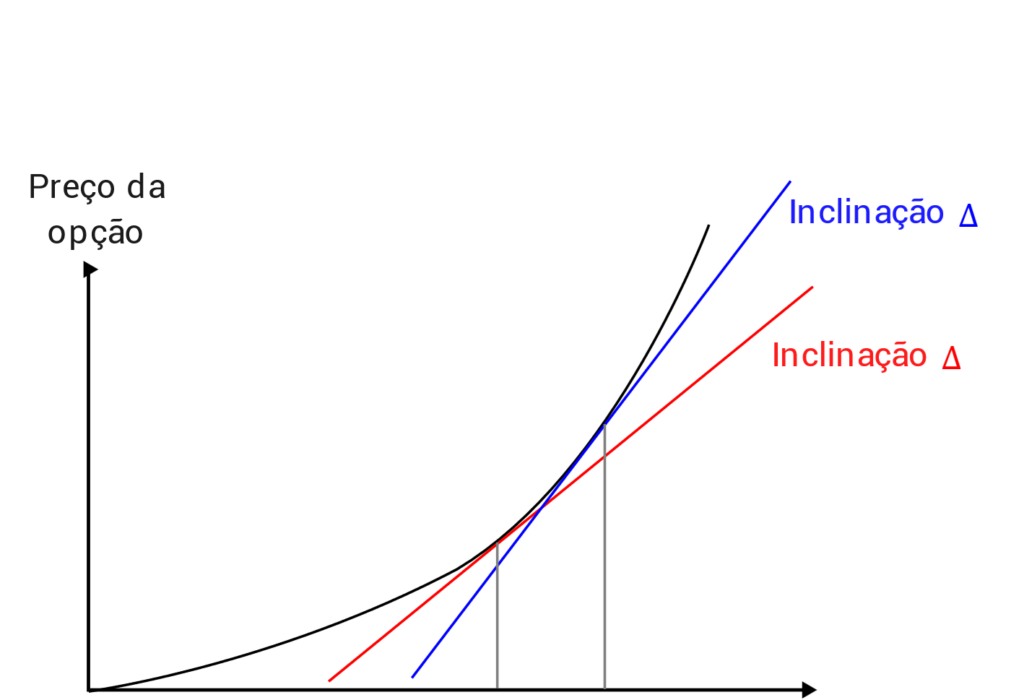
Uma observação importante é que a expressão \(\Delta={{H_{o_n}-L_{o_n}}\over{H_{a_n}-L_{a_n}}}\) que usamos acima, funciona como uma aproximação para o delta, pois a expressão real envolve o uso de derivadas. Apresentamos a expressão correta mais adiante nesse artigo.
Delta de uma put
O preço de uma put diminui à medida que o preço da ação aumenta. Por exemplo:
| Dia | Máxima da ação | Mínima da ação | Máxima da call | Mínima da call | Fechamento da ação | Fechamento da put |
| 1 | 34,71 | 33,85 | 1,05 | 0,73 | 34,13 | 0,95 |
| 2 | 34,62 | 34,07 | 0,94 | 0,75 | 34,21 |
Podemos calcular o \(\Delta\) para o dia 1. Assim:
\[\Delta={{H_{o_n}-L_{o_n}}\over{H_{a_n}-L_{a_n}}}={{1,05-0,73}\over{34,62-34,07}}={{0,32}\over{0,55}}=0,582=58,2\%\]
Com isto, e sabendo que a variação da ação (em preço de fechamento) do dia 1 para o dia 2 foi de R$ 0,08, podemos calcular o novo preço da put que será
\[Preço_{novo}=Preço_{antigo}+\Delta\cdot Variação_{ação}\]
ou seja,
\[Preço_{novo}=R\$0,95+(-0,582)\cdot R\$ 0,08=R\$ 0,95-R\$ 0,05=R\$ 0,90\]
Como esperado, o preço da opção diminuiu com a alta da ação.
Resumo
O delta mede a sensibilidade da variação do preço da opção quando o preço da ação varia.
Quando o delta é positivo, caso das calls, significa que um aumento do preço da ação gera um aumento no preço da opção.
Por outro lado, quando o delta é negativo, significa que um aumento do preço da ação resulta em uma redução no preço da put.
Um ponto importante a se destacar é que o próprio delta muda à medida que o preço da ação varia. A mudança de valor do delta é dada pelo gamma, outra variável do modelo Black & Scholes.
Talvez você também se interesse por:
Para aprofundar
Caso você queira adentrar na matemática do modelo, seguem as fórmulas para o delta de calls e puts
\[\Delta_{call}=N(d_1)\]
e
\[\Delta_{put}=-N(-d_1)=1-N(d_1)\]
em que
\[N(d_1)={{1}\over{\sqrt{2\pi}}\int_{-\infty}^{x}{e^{-{z^2}\over{2}}}dz}\]
é a função de distribuição acumulada normal padrão.
Conheça outras gregas do modelo de Black & Scholes:
