Gamma das opções: acelerando os preços
Se você deseja tornar-se um especialista no mercado de opções, é imprescindível que você conheça o modelo de precificação de Black & Scholes e, em particular, que você conheça as variáveis, ou gregas, do modelo. Uma dessas variáveis é o gamma das opções, que mede a sensibilidade do delta da opção em relação à variação do preço da ação. Se associarmos o delta da opção à velocidade de mudança do preço da opção, então, o gamma seria a aceleração. É sobre essa variável que falaremos no presente artigo.
O que é o gamma
O gamma da opção é a variável que mede a razão entre a mudança do delta da opção e a mudança de preço da ação. Matematicamente,
\[\Gamma={{\Delta_{n}-\Delta_{n-1}}\over{F_{a_n}-F_{a_{n-1}}}}\]
em que
- \(F_{a_n}\) é o preço de fechamento da ação em um determinado pregão .
- \(F_{a_{n-1}}\) é o preço de fechamento da ação no pregão anterior, \(n-1\).
- \(\Delta_{n}\) é o delta da opção em um determinado pregão .
- \(\Delta_{n-1}\) é o delta da opção no pregão anterior, \(n-1\).
Em outras palavras, o \(\Gamma\) é a taxa de variação do em relação à variação do preço da ação. Ou seja, o \(\Gamma\) é a segunda derivada do preço da opção em relação ao preço da ação.
Formalmente falando, o gamma é dado pela equação
\[\Gamma={{N'(d_1)}\over{S\cdot\sigma\sqrt{T-t}}}\]
em que \(N'(d_1)\) é a função densidade de probabilidade normal padrão, \(S\) é o preço do ativo à vista no momento da precificação, ou seja, o spot, \(\sigma\) é a volatilidade da ação, \(T\) é o vencimento e \(t\) é o tempo em anos até o vencimento.
Graficamente
Apresentamos, a seguir, alguns gráficos que relacionam o preço da opção, o delta, o gamma e o preço da ação.
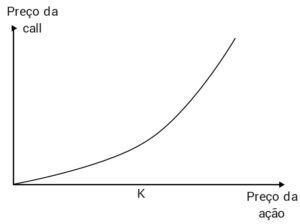
O primeiro gráfico relaciona a variação do preço de uma call em relação à variação do preço da ação. Como você pode ver, essa variação não é linear.
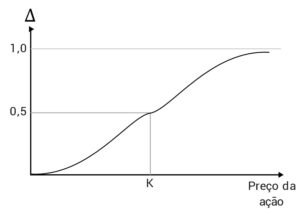
O segundo gráfico, apresenta a variação do delta em relação ao preço da ação. K é o preço de strike da opção. Perceba que o gráfico muda de direção no strike, reduzindo a inclinação. Além disso, ele se aproxima de 1, sem nunca chegar ao valor 1.
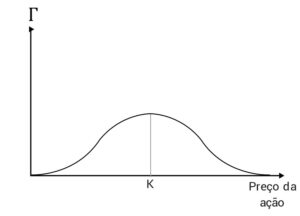
Finalmente, o gráfico acima apresenta a variação do gamma em relação ao preço da ação. K é o preço de strike da opção. Perceba que o valor do gamma é máximo exatamente quando a opção está no dinheiro.
Exemplos
Vejamos alguns exemplos numéricos para um melhor entendimento do papel do gamma.
Exemplo 1
Suponha, por exemplo, que uma ação está valendo R$ 30,00. A call de strike R$ 30,00 possui um delta de 50% e gamma de 20%. O que acontecerá com o delta se a ação subir para R$ 30,10?
Dado que a ação valorizou, então, o delta aumentará. No caso, teremos
\[\Delta_{novo}=\Delta_{Antigo}+\Gamma\cdot Variação_{ação}\]
ou seja
\[\Delta_{novo}=50\%+20\%\cdot0,10=50\%+2\%=52\%\].
Exemplo 2
Suponha que uma ação está valendo R$ 30,00. A call de strike R$ 30,00 possui um delta de 50% e gamma de 20%. O que acontecerá com o delta se a ação cair para R$ 29,60?
Dado que a ação desvalorizou, então, o delta diminuirá. No caso, teremos
\[\Delta_{novo}=\Delta_{Antigo}+\Gamma\cdot Variação_{ação}\]
ou seja
\[\Delta_{novo}=50\%+20\%\cdot(-0,40)=50\%-8\%=42\%\].
 Outras variáveis do modelo de Black & Scholes:
Outras variáveis do modelo de Black & Scholes:
Vega das opções: o efeito da volatilidade na precificação
Theta das opções: compreendendo o tempo como um aliado ou inimigo