Calculando as Gregas em Python
Quando falamos em operações com opções, o cálculo das Gregas é um tópico essencial porque faz parte do operacional de investidores e do dia-a-dia de analistas. Ao selecionar uma opção, devemos considerar não somente suas características de série, mas também as métricas de sensibilidade de opções a variações nas condições de mercado, conhecidas como “As Gregas”. Nesse contexto, é importante conhecer o significado das Gregas e, além disso, saber como podemos calculá-las. Neste artigo, exploraremos calcular as gregas usando Python.
As Gregas e o modelo Black-Scholes
Formalmente, definimos as Gregas em termos das equações de precificação de opções de compra e opções de venda que obtemos a partir do modelo Black-Scholes. Em termos matemáticos, elas consistem na derivada parcial da respectiva função de precificação em relação às variáveis de mercado que participam diretamente da precificação da opção. Essas variáveis são:
- \(S\) é o preço atual do ativo subjacente;
- \(V\) é o preço atual da opção sobre o ativo;
- \(T\) é o tempo de vida restante da opção;
- \(\sigma\) é a volatilidade anual;
- \(r\) é a taxa de juros livre de risco ao ano.
As Gregas, em resumo, medem a variação do preço das opções relativamente a variações em cada um desses parâmetros, individualmente.
O Cálculo das Gregas
Em primeiro lugar, vamos abordar o cálculo das Gregas, utilizando as equações que definem cada uma delas.
Delta
A primeira das Gregas que vamos estudar, o Delta, é uma medida da sensibilidade do preço de uma opção a mudanças no preço do ativo subjacente. O Delta varia em um intervalo de 0 a 1 para opções de compra e de -1 a 0 para opções de venda. Dessa forma, um Delta de 0,50 significa que, para cada aumento de R$ 1,00 no preço do ativo subjacente, o preço da opção de compra aumentará em, aproximadamente, R$0,50. Em contrapartida, um Delta de -0,50 indica que o preço da opção de venda deverá decrescer em R$ 0,50 para cada aumento de R$ 1,00 no preço do ativo subjacente a partir do preço atual.
Em termos matemáticos, Delta é definido como a derivada parcial do preço da opção em relação ao preço do ativo subjacente, ou seja:
\[\Delta={\partial V\over{\partial S}}\]
Em termos práticos, o Delta para uma opção de compra é calculado como
\[\Delta_{call}={\partial V\over{\partial S}}=N(d_1)\]
enquanto que para uma opção de venda temos
\[\Delta_{put}={\partial V\over{\partial S}}=-N(-d_1)\]
em que \(N(\cdot)\) é a função de distribuição de probabilidade acumulada, e
\[d_{1}=\frac{ln\left(\frac{S}{K}\right)+\left(r+\frac{1}{2}\sigma^{2}\right)\cdot T}{\sigma\sqrt{T}}\]
representa a probabilidade relacionada ao exercício da opção no vencimento.
Gamma
O Gamma é uma métrica da variação do Delta de uma opção em relação ao preço do ativo subjacente. Naturalmente, quando o preço do ativo subjacente varia, o Delta também varia. É essa variação no Delta que o Gama representa. O Gamma é relevante para a montagem, avaliação e rebalanceamento de carteiras em estratégias de hedge. Quanto maior Gama, maior o efeito das variações de preço do ativo subjacente sobre o Delta da opção.
Em termos matemáticos, o Gamma é definido como
\[\Gamma=\frac{\partial}{\partial S}\left(\Delta\right)=\frac{\partial^{2}V}{\partial S^{2}}\]
ou seja, a derivada parcial segunda do preço da opção em relação ao preço do ativo subjacente.
Calculando-se essa derivada parcial, obtemos
\[\Gamma=\frac{1}{\sqrt{2\pi}\cdot S\cdot\sigma\cdot\sqrt{T}\cdot e^{\frac{d_{1}^{2}}{2}}}\]
tanto para opções de compra quanto para opções de venda.
Vega
O Vega é uma medida da sensibilidade do preço de uma opção às mudanças na volatilidade esperada do ativo subjacente. A volatilidade esperada reflete as espectativas de mercado em relação à volatilidade futura do ativo subjacente até o vencimento da opção. Essa volatilidade está presente na precificação como volatilidade implícita utilizada para efeito de precificação da opção.
Uma opção com Vega mais elevado é mais sensível às mudanças na volatilidade esperada. Assim, ela é uma escolha atraente para os investidores que acreditam que a volatilidade aumentará.
Em termos matemáticos, Vega é definida como
\[\nu=\frac{\partial V}{\partial\sigma}\]
que resulta em
\[\nu=\frac{S\cdot\sqrt{T}\cdot e^{-\frac{d_{1}^{2}}{2}}}{\sqrt{2\pi}}\]
Theta
O Theta é uma medida da sensibilidade do preço de uma opção ao tempo restante de vida da opção. O passar do tempo tem o efeito de reduzir o valor de uma opção, tendo em vista que o menor horizonte temporal está associado a um menor horizonte de incerteza. Assim, o Theta quantifica essa deterioração do valor da opção com o passar do tempo.
Em termos matemáticos, temos
\[\Theta=\frac{\partial V}{\partial t}\]
que resulta em
\[\Theta=r\cdot V-r\cdot S\cdot\Delta-\frac{1}{2}\cdot\sigma^{2}\cdot S^{2}\cdot\var Gamma.\]
Rho
O Rho é uma medida da sensibilidade do preço de uma opção às mudanças nas taxas de juros. Geralmente, opções de compra têm Rho positivo, o que significa que seus preços aumentam à medida que as taxas de juros sobem. Por outro lado, opções de venda têm Rho negativo, o que significa que seus preços diminuem com o aumento das taxas de juros. No entanto, o impacto do Rho nas opções costuma ser menos significativo em comparação com outras Gregas, a menos que haja mudanças drásticas nas taxas de juros ao longo do tempo de vida da opção.
Em termos matemáticos, Rho é definida como
\[\rho=\frac{\partial V}{\partial r}\]
Temos, portanto
\[\rho=K\cdot T\cdot e^{-rT}\cdot N\left(d_{2}\right)\]
em que
\[d_{2}=d_{1}-\sigma\sqrt{T}\]
está relacionada com a probabilidade de a opção ser exercida em seu vencimento.
Calculando as Gregas em Python
Neste exemplo, vamos considerar o preço inicial do ativo subjacente \(S\left(0\right)=100,00\), o preço de exercício da opção \(K=95,00\), a taxa de juros livre de risco de \(5\%\) ao ano, e tempo de vida igual a 45 dias úteis, ou, \(T=\frac{45}{252}\), para uma volatilidade esperada para o período equivalente a \(\sigma=40\%\) ao ano. O preço atual das opções de compra e venda, calculados através do modelo Black-Scholes: \(C=9,87\) e \(P=4,03\). Com esses dados, vamos calcular as Gregas de uma opção de compra e de uma opção de venda sobre o ativo.
Vamos, então, a um exemplo de rotina para o cálculo de cada uma das Gregas. Em primeiro lugar, precisamos calcular os valores da opção de compra (C) e da opção de venda (P), que são necessários para o cálculo das Gregas. Para isso, podemos utilizar uma implementação do modelo Black-Scholes em forma de uma função, como segue.

A seguir, vamos calcular as Gregas. Para tal, vamos implementar outra função, que podemos chamar de Gregas.

Por fim, incluindo os parâmetros de entrada do modelo, temos:
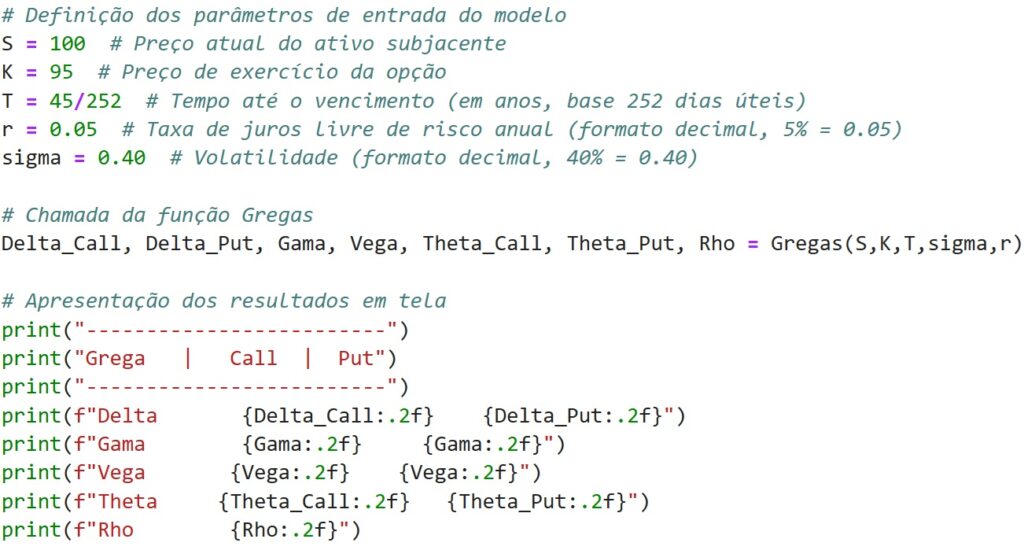
E, pronto! Executando a implementação em Python, devemos ter como resultado os valores das Gregas, conforme mostra a figura.
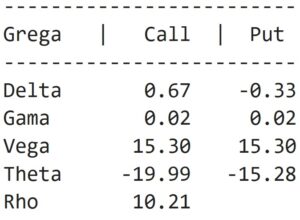
Neste artigo, abordamos brevemente o conceito das Gregas e estudamos um exemplo de como calculá-las usando a linguagem Python. O estudo das Gregas é importante para operar opções, pois permite a leitura rápida do efeito de mudanças nas condições de mercado sobre o preço das opções. Nesse contexto, a linguagem Python é uma das ferramentas mais versáteis por possibilitar não somente o cálculo das Gregas, mas também de diversas outras medidas ou indicadores relevantes para a tomada de decisões informadas nos mercados financeiros.