Usando Python para calcular o prêmio de opções

O modelo Black-Scholes, desenvolvido por Fischer Black, Myron Scholes e Robert Merton na década de 1970, é uma formulação matemática que permite o cálculo do valor esperado de uma opção para um conjunto de condições de mercado. Trata-se do modelo mais utilizado no Mercado Financeiro e que serve como base para a atuação prática de investidores. Portanto, nesse artigo, exploraremos como a linguagem de programação Python pode ser uma ferramenta poderosa para implementar o modelo Black-Scholes e possibilitar o cálculo do prêmio de opções de compra e opções de venda.

O modelo Black-Scholes

A precificação está no cerne da negociação de opções de compra e venda. Isso ocorre porque o preço da opção, que também chamamos de prêmio, é o preço atual da opção no mercado.

A compra de uma opção consiste na compra de um direito de comprar ou vender um ativo subjacente a um preço predeterminado em ou até uma data futura. O prêmio é o valor recebido pelo lançador (vendedor) da opção para assumir a contrapartida, a obrigação de vender ou comprar esse ativo subjacente ao preço predeterminado em uma data futura.

Dados necessários

O modelo Black-Scholes é a metodologia mais amplamente utilizada para a precificação de opções, e é o modelo que implementaremos em Python neste artigo. Para fornecer o “preço teórico” de uma opção de compra ou venda, o modelo requer alguns parâmetros de entrada:

1. Preço do Ativo Subjacente \(S\), que corresponde ao preço atual do ativo financeiro, como uma ação, moeda, índice ou commodity.
2. Preço de Exercício \(K\), que é o preço ao qual o titular da opção tem o direito de comprar (para opções de compra) ou vender (para opções de venda) o ativo subjacente na data de vencimento.
3. Taxa de Juros Livre de Risco \(r\), que corresponde à taxa de juros de títulos do governo de curto prazo, e é usada para descontar os fluxos de caixa futuros associados à opção para seu valor presente.
4. Volatilidade \(\sigma\), que representa a medida da variação do preço do ativo subjacente ao longo do tempo.
5. Tempo de vida da opção \(T\), que corresponde ao período de tempo até a data de vencimento da opção.
6. Taxa de pagamento de dividendos \(d\). No caso das opções negociadas na B3, cujos preços de exercícios são descontados para dividendos, podemos ignorar esse parâmetro. A propósito, formularemos o modelo a seguir desconsiderando a taxa de pagamento de dividendos por esse motivo.

Como usar esses dados?

Tais parâmetros são utilizados em conjunto com as equações de precificação de uma opção de compra, cujo prêmio será denotado por C, e para uma opção de venda, cujo prêmio será denotado por P. Temos, para uma opção de compra,

\[S=S\cdot N(d_1)-K\cdot e^{-rT}\cdot N(d_2)\]

em que \(N(.)\) é a função distribuição acumulada e \(d_{1}\) e \(d_{2}\) são medidas associadas à probabilidade de a opção ser exercida no vencimento, definidas por

\[d_1={{ln({S\over{K}})+(r+{1\over{2}\sigma^2})}\over{\sigma\sqrt{T}}}\]

e

\[d2=d1-\sigma\sqrt{T}\]

Analogamente, para uma opção de venda, o preço \(P\) da opção é dado por

\[P=K\cdot e^{-rT}\cdot N(-d_{2})-S\cdot N(-d_{1})\]

Esses são os elementos necessários para calcularmos o preço teórico de opções de compra e opções de venda. Vamos, a seguir, implementar o modelo Black-Scholes em Python para obter o preço teórico de diversas séries de opções de compra e venda.

Implementando Black-Scholes em Python

Agora, vamos implementar um código para o cálculo do preço de opções de compra e venda usando Python. Você precisará da biblioteca SciPy para calcular a função de distribuição acumulada normal (CDF) e da biblioteca NumPy para operações matemáticas. Vamos também partir de um exemplo.

Exemplo

Neste exemplo, vamos considerar o preço inicial do ativo subjacente \(S\left(0\right)=100,00\), o preço de exercício da opção \(K=95,00\), a taxa de juros livre de risco de \(5\%\) ao ano, e tempo de vida igual a \(45\) dias úteis, ou, \(T={45\over{252}}\), para uma volatilidade esperada para o período equivalente a \(\sigma=40\%\) ao ano.

Em primeiro lugar, definiremos uma função para cálculo do preço de uma opção de compra e de uma opção de venda. A seguir, forneceremos os valores relevantes, como o preço atual do ativo subjacente \(S\), o preço de exercício da opção \(K\), o tempo até o vencimento \(T\), a taxa de juros livre de risco \(r\) e a volatilidade \(\sigma\). O código calculará o preço da opção de compra (call) e o preço da opção de venda (put) com base no modelo Black-Scholes. O código em Python contém os comentários necessários para que a função cumprida por cada trecho da implementação fique esclarecida.

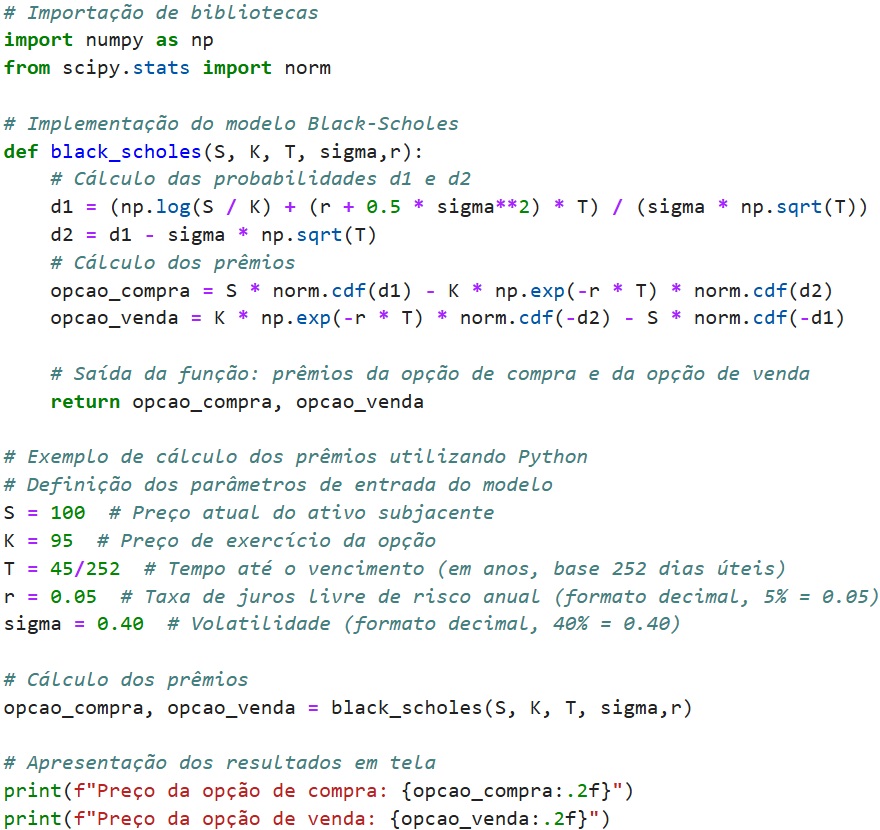
E, pronto! Temos uma implementação do modelo Black-Scholes que calcula o prêmio de opções de compra e de opções de venda. Portanto, podemos explorá-lo utilizando os parâmetros de entrada de nosso interesse. Para nosso exemplo, o preço atual das opções de compra e venda serão de, aproximadamente, \(C=9,87\) e \(P=4,03\).

Talvez você também se interesse por:

Como calcular as gregas das opções

O que mais podemos fazer?

Uma implementação do modelo Black-Scholes em Python oferece uma ampla gama de possibilidades e aplicações para investidores e analistas. Em primeiro lugar, é possível calcular de forma eficiente o preço teórico de opções de compra e venda em diferentes cenários de mercado. Alguns cenários interessantes de simular são aqueles, por exemplo, de alteração nas taxas de juros ou no nível de volatilidade.

Situações inesperadas do mundo real tais como, conflitos, guerras, pandemias, entre outras, podem influenciar enormemente as condições de mercado. Podemos calcular o preço das opções diante de novas e variadas condições utilizando o Python.

Além disso, a flexibilidade e versatilidade da linguagem Python permitem a criação de ferramentas de análise de risco, estratégias de hedge, estratégias de otimização de portfólio, e até mesmo sistemas automatizados de negociação que utilizam o modelo Black-Scholes como base. Diversas bibliotecas estão disponíveis para esses fins, e cabe ao investidor interessado explorá-las e encontrar as ferramentas mais adequadas aos seus objetivos.

Por fim, a vasta gama de bibliotecas financeiras disponíveis, juntamente com a natureza de código aberto do Python, oferecem a flexibilidade necessária para adaptar e estender o modelo Black-Scholes de acordo com as necessidades. Além disso, a integração com visualização de dados e ferramentas estatísticas torna o Python uma boa escolha para a análise de risco, modelagem de estratégias e tomada de decisões no mercado de opções.