Precificação de opções em Python usando o método Monte Carlo

A precificação de opções é uma tarefa fundamental no mundo das finanças, permitindo que investidores avaliem e negociem derivativos com base em uma ampla gama de ativos subjacentes. Uma das abordagens mais versáteis e amplamente utilizadas para a precificação de opções é o método Monte Carlo. Neste artigo, exploraremos como o método Monte Carlo, em Python, é utilizado na importante tarefa de precificar opções.

Preliminares: opções de compra e opções de venda

As opções de compra e as opções de venda são contratos financeiros que concedem ao seu detentor (comprador) o direito, mas não a obrigação, de comprar (para opções de compra) ou vender (para opções de venda) um ativo subjacente a um preço específico (preço de exercício), em ou até uma data futura (data de vencimento). As opções são negociadas no mercado por um preço que corresponde ao valor presente do valor esperado do payoff dessa opção em seu vencimento.

Nesse contexto, precificar uma opção equivale a calcular o “valor justo” do direito representado pelo contrato de opção, descontado para valor presente. Uma das formas de precificar uma opção é utilizando simulações Monte Carlo.

O método Monte Carlo

O método Monte Carlo é uma técnica numérica que utiliza uma grande quantidade de realizações de um processo aleatório, com a finalidade de obter estimativas ou aproximações do comportamento esperado de um sistema ou processo. No caso das opções, o comportamento que se busca modelar é o valor esperado da opção em seu vencimento, e o processo aleatório simulado é a trajetória de preços do ativo subjacente.

Na aplicação do método Monte Carlo à precificação de opções, as trajetórias de preço do ativo subjacente são geradas a partir do preço atual do ativo subjacente e evoluem considerando a volatilidade esperada até o vencimento. Ao final desse processo, aplica-se a função de payoff da opção à “nuvem” de trajetórias simuladas do ativo.

Como resultado, obtemos o valor esperado da opção no vencimento. Descontando-se o valor esperado para valor presente através da taxa de juros livre de risco, temos o “valor justo” da opção de compra ou venda.

Calculando o prêmio de opções usando o método Monte Carlo em Python

Vamos a um passo a passo de uma implementação do método Monte Carlo em Python. Para tal, vamos propor o seguinte problema: para um ativo subjacente com preço atual de R$ 41,75, estimar o “valor justo” de uma opção de compra e de uma opção de venda com preço de exercício de R$ 45,00, a uma taxa de juros de 5% ao ano, com vencimento para daqui a 30 dias úteis e considerando uma volatilidade esperada de 40% ao ano.

Em primeiro lugar, vamos importar as bibliotecas necessárias e definir as variáveis de entrada do problema.

Geração de caminhos aleatórios

Na precificação de opções, podemos interpretar o preço futuro do ativo subjacente como o resultado de um experimento aleatório. Dessa forma, simula-se uma série de caminhos aleatórios para o preço do ativo subjacente usando um modelo estocástico. Assim, cada caminho representa uma possível evolução do preço do ativo ao longo do tempo, a partir do valor atual.

Uma realização do caminho aleatório dos preços do ativo subjacente é obtida iterando-se

\[S\left(k+1\right)=S\left(k\right)e^{\left(r-\frac{1}{2}\sigma^{2}\right)\Delta t+\sigma\sqrt{\Delta t}\omega(k+1)}\]

em que:

• \(S(0)\) é o preço inicial do ativo subjacente;
• \(r\) é o crescimento médio no preço do ativo, geralmente usamos a taxa de juros livre de risco;
• \(\sigma\) é a volatilidade esperada para o ativo no período;
• \(\Delta t\) é o passo da evolução temporal da evolução do preço; e
• \(\omega_{1}, \omega_{2},\omega_{3},…\) é uma variável aleatória independente identicamente distribuída, com média zero e variância unitária.

Denotaremos a i-ésima realização do processo por \(S_{i}\).

Valor da opção no vencimento

Para cada caminho aleatório gerado no passo anterior, calcula-se o valor da opção no vencimento \((T)\). Para opções de compra, o valor é a diferença entre o preço do ativo no vencimento e o preço de exercício, se positivo. Teremos, então, para a i-ésima realização do processo estocástico

\[V_{i}\left(T\right)=max\left(S_{i}\left(T\right)-K,0\right).\]

Para opções de venda, o valor é a diferença entre o preço de exercício e o preço do ativo no vencimento, se positivo, ou seja,

\[V_{i}\left(T\right)=max\left(K-S_{i}\left(T\right),0\right).\]

Caso contrário, o valor é zero, ou seja, a opção “vira pó” no vencimento.

 

Média dos valores das opções

Nesta etapa, calcula-se a média dos payoffs obtidos na etapa anterior. Considerando que todos os caminhos aleatórios são equiprováveis, considera-se, para esse fim, a média aritmética simples. O valor obtido pelo cálculo da média representa o valor esperado da opção no vencimento. No caso de \(n\) realizações do processo

\[E\left[V\left(T\right)\right]=\bar{V}\left(T\right)=\frac{1}{n}\sum_{i=1}^{n}V_{i}\left(T\right)\]

Para que o valor esperado aproxime-se do preço teórico da opção, é necessário utilizar um número grande de trajetórias.

Desconto para valor presente

A média obtida na etapa anterior corresponde, aproximadamente, ao valor esperado do payoff da opção no vencimento. Devemos descontar o valor esperado para o presente usando a taxa de juros livre de risco para estimar o preço atual da opção.

Obter o preço atual da opção conclui o processo de precificação, que é justamente o cálculo do valor presente do payoff esperado da opção. Assim, para uma taxa de juros livre de risco \(r\), em regime de capitalização contínua, temos

\[V\left(t\right)=e^{-r\left(T-t\right)}E\left[V\left(T\right)\right].\]

Como resultado, encontraremos os valores aproximados de R$ 1,18 para a opção de compra e de R$ 4,16 para a opção de venda. Por fim, podemos fazer um gráfico representando as trajetórias simuladas.

 

E assim, temos nossa implementação do método Monte Carlo na linguagem Python, e podemos estimar o preço de opções de compra e opções de venda. Para resultados mais próximos àqueles obtidos utilizando o modelo Black-Scholes, devemos utilizar um número grande de realizações (variável n_paths), possivelmente algo em torno das dezenas de milhares.

 

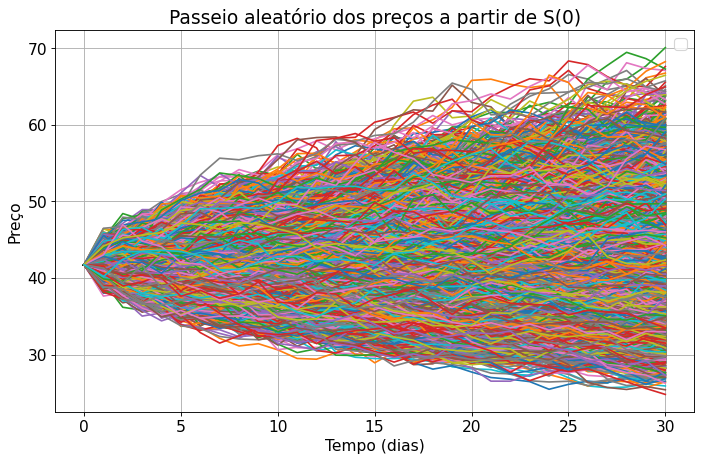
Em resumo, na precificação de opções usando o método Monte Carlo e a linguagem Python, estamos gerando caminhos aleatórios para o preço do ativo subjacente e calculando o valor presente da média dos payoffs das opção no vencimento. Para opções mais complexas e que envolvem condições personalizadas, tais como as opções exóticas, precisamos modelar o comportamento da opção, de forma a incluir essas condições no modelo a ser avaliado.

Por fim, o método Monte Carlo é uma ferramenta versátil e poderosa para a precificação de opções e uma ampla variedade de outros problemas financeiros. A linguagem Python, por sua vez, é versátil, de fácil leitura e com uma ampla comunidade e documentação disponíveis. Utilizando ambas, podemos ampliar as possibilidades de acesso a informações relevantes para as tomadas de decisões no Mercado Financeiro.